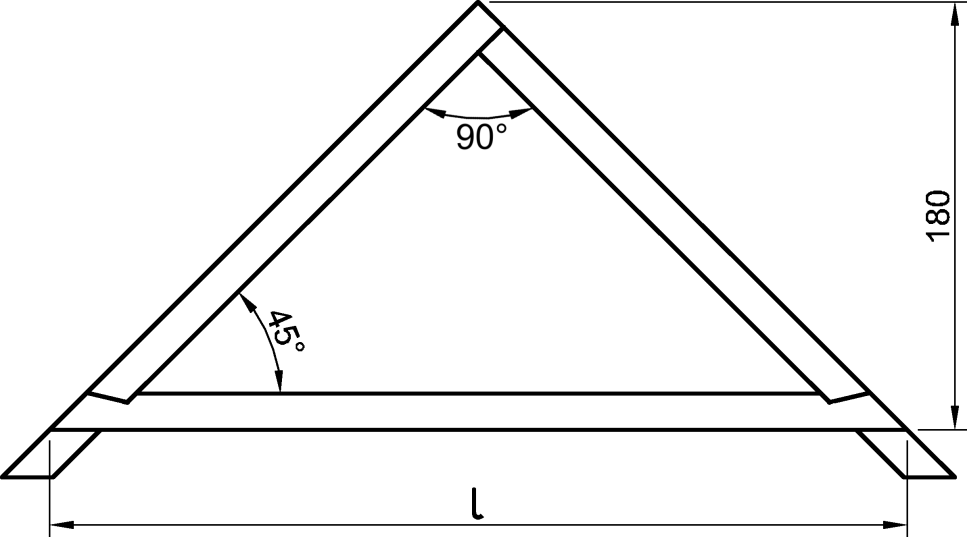
Dobrze to rozpracowane. W tego typu konstrukcji więźby dachowej, gdzie kąt nachylenia krokwi wynosi 45°, kluczowa jest znajomość zależności trygonometrycznych w trójkącie prostokątnym. Jeżeli odległość jętki od kalenicy wynosi 1,8 m (czyli 180 cm, jak na rysunku), to odcinek między jętkami można policzyć jako dwukrotność tej odległości, bo jętka znajduje się symetrycznie po obu stronach połaci. Przy kącie 45° długość krokwi od kalenicy do jętki jest równa pionowej wysokości (1,8 m), a więc poziomy rozstaw jętek (długość jętki) to 2 × 1,8 m, czyli właśnie 3,60 m. To jest bardzo praktyczna wiedza, bo w branży budowlanej często stosuje się takie uproszczenia – konstruktorzy lub cieśle posługują się kątem 45°, żeby łatwiej liczyć długości elementów więźby. Ma to też ścisły związek z normami dotyczącymi geometrii dachów, gdzie kąty 45° pozwalają na przewidywalne rozkłady sił i łatwiejszy dobór przekrojów drewna. Widać, że w praktyce bardzo przydaje się szybkie kojarzenie tych zależności, bo na placu budowy nikt nie będzie wyciągał kalkulatora do każdego pomiaru. Moim zdaniem warto ćwiczyć takie przypadki na różnych kątach, bo to rozwija techniczne myślenie i przygotowuje do realnych wyzwań.
W zadaniu tym pojawia się kilka typowych pułapek, które łatwo mogą doprowadzić do niewłaściwego wyniku. Po pierwsze, trzeba pamiętać, że nachylenie krokwi pod kątem 45° oznacza, że trójkąt powstały z połowy więźby jest trójkątem prostokątnym równoramiennym. To pozwala bardzo szybko powiązać długość pionową z poziomą – w tym przypadku odległość od kalenicy do jętki jest równa połowie długości jętki. Częsty błąd to mylenie długości krokwi z długością jętki albo przeliczanie długości po skosie zamiast po poziomie. Czasem ktoś próbuje policzyć długość jętki za pomocą wzorów na przekątną lub korzysta z funkcji trygonometrycznych, lecz źle dobiera dane – np. bierze pod uwagę całą wysokość więźby, a nie tylko odcinek od kalenicy do jętki. Inna pomyłka to niewłaściwe przeliczenie jednostek (metry zamiast centymetrów lub odwrotnie) albo zaakceptowanie zbyt dużej wartości, którą teoretycznie mogłaby mieć krokwia, ale nie jętka. W praktyce spotyka się też zwyczajowe zaokrąglanie wyników, co prowadzi do błędnych oszacowań. Jeżeli ktoś wybrał odpowiedź znacznie odbiegającą od 3,60 m, najpewniej nie uwzględnił faktu, że długość jętki przy 45° to po prostu dwukrotność tej odległości od kalenicy, bo taki jest układ geometryczny tej więźby. Warto w przyszłości dokładnie analizować, które odcinki są poszukiwane i jaką rolę pełni dany element w konstrukcji, a nie sugerować się tylko liczbami z tabel czy kalkulatora. To klucz do poprawnych obliczeń w pracy przy więźbach dachowych.