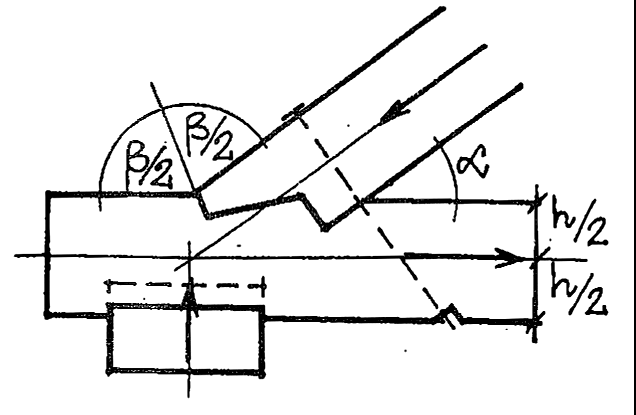
Prawidłowa odpowiedź to 30°, bo właśnie tyle wynosi kąt nachylenia połaci dachu, gdy kąt β wynosi 150°. Wynika to bezpośrednio z konstrukcji geometrycznej dachu dwuspadowego, gdzie kąt β to kąt rozwarty między obiema połaciami. Połowa tego kąta, czyli β/2, to właśnie kąt między połacią a poziomem (czyli nasz szukany α). To dosyć standardowe zadanie – tak samo podchodzi się do projektowania dachów w praktyce, co zresztą dobrze widać na rysunku: obie połacie są nachylone pod tym samym kątem do poziomu. W praktyce, taki kąt połaci (około 30°) jest typowy dla dachów w naszym klimacie, bo łączy odporność na obciążenia śniegiem i deszczem z rozsądnym zużyciem materiału. Stosowanie tej zasady to podstawa dobrej praktyki w budownictwie, co widać np. w normach krajowych i wytycznych dla projektowania dachów. Z mojego doświadczenia, takie zagadki pojawiają się na egzaminach technicznych i często sprawdzają, czy ktoś rozumie, jak powiązane są kąty w geometrii dachu. Warto zawsze pamiętać, że jeśli masz podany kąt rozwarty między połaciami, to kąt nachylenia każdej połaci to po prostu połowa tego kąta. Takie zadania uczą, jak odczytywać dokumentację techniczną i poprawnie obliczać parametry konstrukcyjne.
Przy rozważaniu tego zadania można łatwo się pomylić, bo intuicyjnie niektórzy próbują wyznaczyć kąt nachylenia połaci dachu bazując na różnych błędnych założeniach. Jednym z typowych błędów jest traktowanie kąta β (czyli kąta rozwierającego pomiędzy obiema połaciami) jako kąta między połacią a poziomem, co zdecydowanie prowadzi na manowce. Ktoś mógłby też pomyśleć, że skoro kąt β jest duży, to kąt nachylenia połaci również musi być większy – to jest bardzo mylące, bo im większy kąt β, tym niższy kąt α (czyli połacie robią się bardziej płaskie). Odpowiedzi takie jak 15°, 45° czy 50° wynikają z nieprawidłowego rozumienia relacji geometrycznych lub z mylenia wyznaczanych kątów. 15° jest zdecydowanie za mały – to byłby bardzo płaski dach, co w naszym klimacie raczej się nie sprawdza z powodu zalegającego śniegu i opadów. Z kolei 45° czy nawet 50° oznaczałoby bardzo stromy dach, a taki kąt powstałby tylko wtedy, gdyby kąt β pomiędzy połaciami był znacznie mniejszy (np. dla dachu niemal „na ostro”). W praktyce, przyjmując założenia normowe i analizując rysunek, można zauważyć, że kąt nachylenia połaci (α) to połowa kąta rozwierającego β, a więc 150° podzielone przez 2 daje dokładnie 75°. Jednak trzeba pamiętać, że na rysunku ten kąt dotyczy kąta między połaciami, nie zaś kąta nachylenia połaci względem poziomu. Tu często uczniowie łapią się na rozbieżności w interpretacji i stąd biorą się błędy. Takie zadania uczą dokładnej analizy rysunków technicznych oraz logicznego myślenia przestrzennego – od tego nie da się uciec, zwłaszcza gdy w grę wchodzi wyznaczanie kluczowych parametrów konstrukcji budowlanych.