Wyniki egzaminu

Nowy egzamin

Informacje o egzaminie:

Zawód: Technik geodeta
Kwalifikacja: BUD.18 - Wykonywanie pomiarów sytuacyjnych, wysokościowych i realizacyjnych oraz opracowywanie wyników tych pomiarów
Data rozpoczęcia: 25 stycznia 2026 12:10
Data zakończenia: 25 stycznia 2026 12:45

Egzamin zdany!

Wynik: 22/40 punktów (55,0%)

Wymagane minimum: 20 punktów (50%)

Pochwal się swoim wynikiem!

Facebook

X.com

Szczegółowe wyniki:

Pytanie 1

Na łatach niwelacyjnych umiejscowionych w punktach 100 oraz 101 dokonano pomiarów l₁₀₀ = 1 555, l₁₀₁ = 2 225. Jaka jest różnica wysokości Δh_100-101 między punktami 100 a 101?

A. -0,670 m

B. 0,670 m

C. -0,670 cm

D. 6,700 m

Wybór odpowiedzi, która nie jest zgodna z poprawnym wynikiem, może wynikać z kilku typowych błędów myślowych związanych z interpretacją odczytów niwelacyjnych. W przypadku błędnych odpowiedzi, takich jak 6,700 m, można zauważyć, że wynika to z mylnego założenia, iż obliczenia należy wykonać w jednostkach niezwiązanych z rzeczywistą różnicą wysokości. To podejście ignoruje fakt, że różnice wysokości powinny być podawane w metrach, a nie w centymetrach. Odpowiedzi, które sugerują zmiany w wysokości, są często wynikiem nieprawidłowego zrozumienia sposobu działania niwelacji, gdzie kluczowe jest rozróżnienie między odczytem wysokości a rzeczywistą różnicą wysokości między punktami. Warto również zwrócić uwagę na jednostki. Odpowiedź -0,670 cm jest niepoprawna, ponieważ zamiast tego powinno być -0,670 m. Użycie nieodpowiednich jednostek może prowadzić do dramatycznych różnic w interpretacji danych geodezyjnych. Kluczowe w tej dziedzinie jest przestrzeganie właściwych norm oraz praktyk, które wymagają, aby wyniki były jednoznaczne i precyzyjnie wyrażone w standardowych jednostkach miary. W związku z tym, aby uniknąć takich pomyłek, istotne jest zrozumienie podstawowych zasad niwelacji oraz poprawne stosowanie wzorów i jednostek. W praktyce geodezyjnej, znajomość odpowiednich norm i procedur jest niezbędna dla uzyskania dokładnych wyników pomiarów.

Pytanie 2

Jaki dokument geodezyjny jest kluczowy do zlokalizowania w terenie punktu osnowy geodezyjnej?

A. Szkic przeglądowy

B. Opis topograficzny punktu

C. Dziennik pomiaru boków osnowy

D. Dziennik pomiaru kątów osnowy

Opis topograficzny punktu jest kluczowym dokumentem geodezyjnym, który zawiera wszelkie istotne informacje o lokalizacji punktu osnowy geodezyjnej. Dokument ten zazwyczaj zawiera szczegółowy opis otoczenia punktu, w tym jego położenie w terenie, charakterystykę sąsiednich obiektów oraz wskazówki dotyczące dotarcia do punktu. Dzięki tym informacjom geodeta może precyzyjnie zlokalizować punkt osnowy, co jest niezbędne do przeprowadzania dalszych pomiarów i prac geodezyjnych. W praktyce, opis topograficzny jest często stosowany w projektach, gdzie precyzyjne pomiary są kluczowe, jak w inżynierii lądowej czy planowaniu przestrzennym. Standardy geodezyjne, takie jak normy ISO oraz krajowe przepisy dotyczące geodezji, wskazują na konieczność sporządzania takich opisów, co podkreśla ich znaczenie w branży. Dobrą praktyką jest także sporządzanie aktualizacji opisu topograficznego, zwłaszcza w rejonach intensywnie rozwijających się, aby zapewnić, że informacje pozostają aktualne.

Pytanie 3

Jeśli dokonano poniższych pomiarów kąta pionowego: w pierwszym ustawieniu lunety KL = 83,3400g oraz w drugim ustawieniu lunety KP = 316,6700g, to wartość kąta nachylenia α wynosi

A. 83,3400g

B. 83,3350g

C. 16,6650g

D. 16,6700g

Analizując błędne odpowiedzi, warto zauważyć, że w kontekście obliczania kąta nachylenia α podstawową zasadą jest prawidłowe zrozumienie, czym jest różnica pomiędzy dwoma odczytami lunety. Wybór wartości 83,3350g sugeruje jedynie nieznaczne obniżenie jednego z odczytów, co nie ma logicznego uzasadnienia w kontekście geodezyjnym. Odczyt 83,3400g odnosi się do położenia I lunety, natomiast w położeniu II mamy wartość 316,6700g. Błędne podejście polega na zignorowaniu właściwej metody obliczania różnicy, co prowadzi do mylnego wniosku. Odpowiedź 16,6700g także wydaje się być bliska prawdy, lecz nie uwzględnia różnicy między wyjściowymi odczytami. Istotnym błędem jest także to, że nie wszyscy uwzględniają, iż kąty nachylenia w geodezji są wyrażane jako różnice między odczytami w odniesieniu do poziomu. Z kolei wartość 83,3400g jest jedynie powtórzeniem odczytu z położenia I, co w żaden sposób nie odnosi się do obliczenia kąta nachylenia. W geodezji, dla poprawności pomiarów i analiz, kluczowe jest stosowanie właściwych formuł i zrozumienie kontekstu, w jakim są używane, dlatego tak ważne jest przyswajanie wiedzy na temat standardów i dobrych praktyk w tej dziedzinie.

Pytanie 4

Który z poniższych instrumentów geodezyjnych służy do pomiaru kątów poziomych i pionowych?

A. Niwelator

B. Inklinometr

C. Teodolit

D. Tachimetr

Niwelator jest instrumentem geodezyjnym, który służy głównie do wykonywania pomiarów wysokościowych. Używa się go przede wszystkim do określania różnic wysokości między punktami, co jest kluczowe przy niwelacji terenu. O ile niwelator jest nieoceniony przy pomiarach pionowych, nie jest narzędziem przeznaczonym do pomiaru kątów poziomych i pionowych, jak teodolit. Tachimetr to bardziej zaawansowane urządzenie, które łączy funkcje teodolitu i dalmierza, umożliwiając pomiary kątów oraz odległości. Choć tachimetry mogą również mierzyć kąty, ich głównym zastosowaniem jest szybkie i dokładne wykonywanie pomiarów terenowych, łącząc różne funkcje w jednym urządzeniu. Tachimetry są bardzo popularne, jednak nie są stricte przeznaczone tylko do pomiaru kątów, co różni je od teodolitów. Inklinometr, z kolei, to instrument używany do pomiaru nachylenia lub kąta w stosunku do poziomu odniesienia, ale nie do pomiaru kąta poziomego i pionowego. Może być stosowany w różnych dziedzinach, od geotechniki po przemysł naftowy, ale jego funkcja jest specyficzna i nie obejmuje pomiarów kątów w sposób, w jaki robi to teodolit. W przypadku analizowanych odpowiedzi, podstawowym błędem jest niewłaściwe przypisanie funkcji pomiarowych tych instrumentów, co może prowadzić do nieporozumień w zastosowaniach praktycznych.

Pytanie 5

Jaką wartość ma azymut przeciwny do azymutu wynoszącego 327^g12^c35^cc?

A. 27g12c35cc

B. 127g12c35cc

C. 527g12c35cc

D. 227g12c35cc

Zrozumienie koncepcji azymutu oraz jego odwrotności jest kluczowe w nawigacji i geodezji. Błędne odpowiedzi zazwyczaj wynikają z niepoprawnych obliczeń lub zrozumienia zasady konwersji azymutów. Na przykład, odpowiedź 27°12'35'' mogłaby sugerować, że osoba myli zakres azymutów lub nie dodaje 180° odpowiednio. W rzeczywistości, 27° byłoby znacznie poniżej połowy okręgu, a tym samym niewłaściwą interpretacją azymutu odwrotnego. Kolejny błąd, który możemy zauważyć, to odpowiedź 527°12'35''. Wartości azymutów nie mogą przekraczać 360°, dlatego takie podejście jest niewłaściwe. Podobnie, odpowiedź 227°12'35'' wskazuje na błędne zrozumienie dodawania 180° do azymutu, co skutkuje rozwiązaniem, które nie jest zgodne z zasadami obliczeń nawigacyjnych. Główne błędy myślowe związane z tymi odpowiedziami to nieprawidłowe dodawanie składników azymutu lub ignorowanie zasad konwersji w zakresie 0°-360°. Aby prawidłowo obliczyć azymut odwrotny, należy zawsze dodać 180° do pierwotnego azymutu i, jeśli to konieczne, dostosować wynik w taki sposób, aby pozostał w dozwolonym zakresie. W praktyce, umiejętność ta jest wykorzystywana nie tylko w nawigacji, ale i w geodezji, gdzie precyzyjne określenie kierunku jest niezbędne do pomiarów i planowania przestrzennego.

Pytanie 6

Aby zaktualizować część mapy zasadniczej, geodeta powinien uzyskać informacje

A. z ewidencji gruntów oraz budynków

B. z państwowego zasobu geodezyjnego i kartograficznego

C. z urzędu miasta

D. z urzędu wojewódzkiego

Odpowiedź "z państwowego zasobu geodezyjnego i kartograficznego" jest prawidłowa, ponieważ to właśnie ten zasób stanowi kompleksowe źródło aktualnych i wiarygodnych danych geodezyjnych i kartograficznych, które są niezbędne do aktualizacji mapy zasadniczej. W Polsce państwowy zasób geodezyjny i kartograficzny jest gromadzony i udostępniany przez Główny Urząd Geodezji i Kartografii (GUGiK), a jego zawartość obejmuje m.in. dane o granicach nieruchomości, infrastrukturze oraz elementach zagospodarowania przestrzennego. Przykładowo, przy aktualizacji mapy zasadniczej, geodeta powinien korzystać z ortofotomap oraz modelu 3D, które są dostępne w ramach tego zasobu. Warto też zaznaczyć, że korzystanie z państwowego zasobu geodezyjnego i kartograficznego jest zgodne z obowiązującymi przepisami prawa, w tym Ustawą z dnia 17 maja 1989 r. – Prawo geodezyjne i kartograficzne, co zapewnia rzetelność i aktualność pozyskiwanych danych, co jest kluczowe dla precyzyjnego odwzorowania rzeczywistości na mapach.

Pytanie 7

To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 8

W związku z wymaganiami precyzyjności pomiaru, szczegóły terenowe klasyfikowane są w trzy

A. grupy

B. kategorie

C. rodzaje

D. klasy

Podział szczegółów terenowych na grupy jest podstawowym elementem w organizacji i analizie danych terenowych, co jest kluczowe w geodezji oraz naukach przyrodniczych. Grupy te są definiowane na podstawie cech takich jak dokładność, typ terenu czy zastosowanie. W praktyce, klasyfikacja szczegółów terenowych na grupy umożliwia inżynierom i geodetom skuteczne planowanie pomiarów i analizę wyników. Na przykład, w geodezji inżynieryjnej, szczegóły mogą być podzielone na grupy w zależności od ich wpływu na projekt budowlany, co pozwala na optymalizację kosztów i czasu realizacji. W standardach geodezyjnych, takich jak normy ISO, podkreślana jest konieczność precyzyjnego określenia grup w celu zapewnienia jednolitości w zbieraniu i interpretacji danych, co jest niezbędne dla uzyskania wiarygodnych wyników.

Pytanie 9

Który z błędów instrumentalnych teodolitu nie jest usuwany podczas pomiaru kąta w dwóch pozycjach lunety?

A. Położenie zera

B. Libella rurkowa

C. Inklinacja

D. Kolidacja

Libella rurkowa jest elementem teodolitu, który odpowiada za poziomowanie instrumentu. W przypadku błędu instrumentalnego związanego z libellą rurkową, jego eliminacja nie jest możliwa poprzez pomiar kątów w dwóch położeniach lunety. Działa to w ten sposób, że błędy wynikające z nieprawidłowego ustawienia poziomu nie mogą być skorygowane przez zmianę pozycji pomiarowej, ponieważ poziom jest określany niezależnie od orientacji lunety. W praktyce oznacza to, że jeśli libella jest źle skalibrowana, to błędy będą się powtarzać niezależnie od tego, jak często zmieniamy pozycję lunety. Dlatego tak ważne jest regularne sprawdzanie i kalibracja libelli rurkowej przed rozpoczęciem pomiarów. W standardach takich jak norma ISO 17123-1 określono procedury kalibracyjne, które powinny być przestrzegane, aby zapewnić dokładność pomiarów. Użycie teodolitu, w tym jego libelli, w geodezji, budownictwie czy inżynierii lądowej wymaga staranności, aby uniknąć błędów, które mogą prowadzić do poważnych konsekwencji w planowaniu i realizacji projektów budowlanych.

Pytanie 10

Wskazanie lokalizacji pikiet w terenie oznacza zdefiniowanie miejsca, w którym podczas dokonywania pomiaru

A. powinno być ustawione lustro lub łata

B. powinno znajdować się stanowisko instrumentu

C. powinien być pomiarowy

D. powinien znajdować się obserwator

Wybór odpowiedzi, które nie odnosi się do ustawienia lustra lub łaty, wskazuje na nieporozumienie dotyczące podstawowych zasad pomiarów geodezyjnych. Odpowiedzi sugerujące, że obserwator czy pomiarowy powinien stać w danym miejscu, są błędne, ponieważ nie uwzględniają roli narzędzi pomiarowych w procesie zbierania danych. Obserwator nie jest odpowiedzialny za bezpośrednie pomiary, lecz pełni rolę nadzorczą, weryfikując poprawność ustawienia sprzętu. Ponadto, wskazanie, że stanowisko instrumentu powinno znajdować się w konkretnym miejscu, jest mylące, ponieważ kluczowe jest, aby instrument był skierowany na lustro bądźłatę, a nie tylko znajdował się w określonym punkcie. Zrozumienie, że lustro/łata to elementy, które odpowiadają za właściwe odczyty, jest fundamentalne dla prawidłowego przeprowadzania pomiarów. Właściwe ustawienie instrumentu jest ważne, lecz to interakcja między instrumentem a lustrem/łatą decyduje o dokładności pomiarów. Mylenie roli poszczególnych elementów może prowadzić do poważnych błędów w obliczeniach i interpretacji wyników, co jest nieakceptowalne w praktyce geodezyjnej. Zgodne z normami pomiarowymi, kluczowe jest, aby każdy z elementów procesu pomiarowego był właściwie zrozumiany i stosowany, aby zapewnić wiarygodność i dokładność uzyskiwanych danych.

Pytanie 11

Który z poniższych błędów nie jest usuwany przez pomiar z punktu centralnego w niwelacji geometrycznej?

A. Refrakcja pionowa.

B. Osadzenie instrumentu.

C. Różne położenie zera pary łat.

D. Zakrzywienie powierzchni ziemi.

Osiadanie instrumentu jest zjawiskiem, które może wystąpić, jeśli sprzęt nie jest prawidłowo umiejscowiony lub jeśli podłoże, na którym stoi, nie jest stabilne. Taki błąd można zminimalizować poprzez odpowiednie przygotowanie stanowiska pomiarowego, ale nie eliminuje go całkowicie. Refrakcja pionowa to zjawisko, które wpływa na przebieg promieni świetlnych w atmosferze, co może wprowadzać błędy w pomiarach geodezyjnych. Nawet mając na uwadze refrakcję, niwelacja geometryczna nie jest w stanie jej całkowicie wyeliminować, chociaż można stosować korekty w obliczeniach. Zakrzywienie powierzchni ziemi to kolejny czynnik, który należy brać pod uwagę, szczególnie na dużych odległościach, gdzie jego wpływ staje się zauważalny. Użycie metod niwelacyjnych wymaga uwzględnienia wszystkich tych zjawisk, lecz nie można ich wyeliminować jedynie poprzez pomiar ze środka. Często w praktyce geodezyjnej występuje mylne przekonanie, że odpowiedni pomiar ze środka rozwiąże wszystkie problemy związane z pomiarami, co jest błędne. W rzeczywistości, każdy z tych błędów wymaga innego podejścia i zastosowania odpowiednich metod korekcyjnych, aby uzyskać wiarygodne wyniki pomiarów.

Pytanie 12

To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 13

Jakie jest wartość azymutu odcinka AB, jeśli współrzędne punktów A i B to: Y_A = 100,00; X_A = 100,00; Y_B = 150,00; X_B = 50,00?

A. 135°

B. 225°

C. 315°

D. 45°

W przypadku błędnych odpowiedzi często pojawiają się mylne interpretacje dotyczące kierunków, które mogą prowadzić do nieprawidłowych obliczeń azymutu. Na przykład, wartości 45°, 315° i 225° mogą być wynikiem błędnych obliczeń lub niepoprawnej interpretacji kierunków. Azymut 45° oznaczałby kierunek północno-wschodni, co nie odpowiada rzeczywistemu położeniu punktu B w stosunku do punktu A, ponieważ punkt B leży na południowym zachodzie względem punktu A. Z kolei azymut 225° wskazuje kierunek południowo-zachodni, co również jest niezgodne z danymi współrzędnymi, gdzie B jest w rzeczywistości wyżej w osi Y, ale dalej w osi X. Azymut 315° z kolei sugeruje kierunek północno-zachodni, co jest błędne, gdyż nie uwzględnia faktu, że z punktu A do punktu B należy poruszać się w dół i w lewo. Kluczowym błędem myślowym jest niepoprawne rozumienie różnicy między azymutem a kierunkiem, co może prowadzić do pomyłek w obliczeniach. Ważne jest, aby przed przystąpieniem do obliczeń dokładnie zrozumieć, jak współrzędne wpływają na wyznaczane kierunki oraz aby stosować poprawne metody obliczania, które uwzględniają zarówno wartości X, jak i Y. W geodezji i kartografii, gdzie precyzja i poprawność kierunków są kluczowe, takie błędy mogą prowadzić do poważnych konsekwencji w analizach przestrzennych.

Pytanie 14

Na podstawie przedstawionych w ramce przepisów prawnych określ, ile wynosi minimalna dokładność określenia położenia pojedynczego drzewa względem poziomej osnowy pomiarowej podczas pomiaru sytuacyjnego?

§ 16. Geodezyjny pomiar sytuacyjny

Geodezyjny pomiar sytuacyjny wykonuje się w sposób zapewniający określenie położenia szczegółu terenowego względem punktów poziomej osnowy geodezyjnej lub pomiarowej, z dokładnością nie mniejszą niż:

1) 0,10 m - w przypadku szczegółów terenowych I grupy;

2) 0,30 m - w przypadku szczegółów terenowych II grupy;

3) 0,50 m - w przypadku szczegółów terenowych III grupy;

[...]

§ 20. Geodezyjny pomiar wysokościowy

Geodezyjny pomiar wysokościowy wykonuje się w sposób zapewniający określenie wysokości szczegółu terenowego względem punktów wysokościowej osnowy geodezyjnej lub pomiarowej, z dokładnością nie mniejszą niż:

1) 0,02 m - dla przewodów i urządzeń kanalizacyjnych, o których mowa w § 19 ust. 3 pkt 1 i 2;

2) 0,05 m - dla obiektów budowlanych i urządzeń budowlanych oraz pikiet markowanych w terenie;

3) 0,1 m - dla budowli ziemnych, elastycznych lub mierzonych elektromagnetycznie podziemnych obiektów sieci uzbrojenia terenu oraz pikiet niemarkowanych w terenie.

A. 10 cm

B. 50 cm

C. 5 cm

D. 30 cm

Odpowiedź 30 cm jest prawidłowa, gdyż zgodnie z § 16. Geodezyjny pomiar sytuacyjny, minimalna dokładność określenia położenia szczegółów terenowych II grupy, do których zaliczają się drzewa, wynosi 0,30 m (30 cm). W praktyce oznacza to, że przy pomiarze sytuacyjnym położenie pojedynczego drzewa powinno być określone z dokładnością umożliwiającą jego jednoznaczne zlokalizowanie w terenie. W kontekście geodezyjnym wymagana dokładność jest istotna nie tylko dla celów inwentaryzacyjnych, ale również dla późniejszego zagospodarowania terenu. Na przykład, w przypadku projektów budowlanych, dokładność ta ma kluczowe znaczenie dla planowania układu drogowego czy lokalizacji innych obiektów. Warto również zauważyć, że takie normy wynikały z analizy potrzeb użytkowników danych przestrzennych oraz z praktycznych zastosowań w geodezji i kartografii, co zapewnia nie tylko precyzję, ale także wiarygodność danych.

Pytanie 15

Zbiór punktów o współrzędnych X, Y ustalonych w sieciach geodezyjnych o najwyższej precyzji określamy mianem osnowy

A. niwelacyjną

B. dokładną

C. pomiarową

D. podstawową

Zrozumienie pojęcia osnowy geodezyjnej jest kluczowe dla prawidłowego podejścia do zagadnień pomiarowych. Wybór nieadekwatnych terminów, takich jak osnowa szczegółowa, niwelacyjna, czy pomiarowa, może prowadzić do istotnych nieporozumień. Osnowa szczegółowa odnosi się do lokalnych układów współrzędnych, które są wykorzystywane w bardziej precyzyjnych pomiarach, ale nie mają tego samego znaczenia co osnowa podstawowa. Osnowa niwelacyjna dotyczy pomiarów wysokości, bazując na poziomach referencyjnych, co jest zaledwie jednym z aspektów geodezji, a nie całościowym podejściem do układu współrzędnych. W kontekście osnowy pomiarowej, jest to termin ogólny, który nie odnosi się do specyficznych, precyzyjnych punktów, jak ma to miejsce w przypadku osnowy podstawowej. Typowe błędy myślowe polegają na myleniu tych pojęć i przypisywaniu im rangi, której nie powinny mieć, co może skutkować poważnymi konsekwencjami w zakresie jakości i dokładności pomiarów. W praktyce, niezrozumienie różnic pomiędzy tymi rodzajami osnowy może prowadzić do błędów w projektowaniu i wykonaniu prac geodezyjnych, co z kolei wpływa na dalsze procesy inżynieryjne oraz planistyczne.

Pytanie 16

To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 17

Jakiego typu przyrządów geodezyjnych należy użyć do przeprowadzenia pomiarów w metodzie tachimetrii klasycznej?

A. Teodolitu oraz tyczki

B. Teodolitu oraz łaty niwelacyjnej

C. Niwelatora oraz łaty niwelacyjnej

D. Niwelatora oraz tyczki

Wybór niepoprawnych zestawów przyrządów geodezyjnych często wynika z niepełnego zrozumienia metod pomiarowych. Na przykład, niwelator i tyczka są używane do pomiarów wysokości, ale nie pozwalają na precyzyjne pomiary kątów, co jest kluczowe w tachimetrii. Niwelator służy głównie do poziomowania i ustalania różnic wysokości, lecz nie może być użyty do określenia kątów poziomych. Dlatego jego użycie w kontekście tachimetrii jest niewłaściwe, gdyż nie dostarcza wszystkich niezbędnych danych do pełnej analizy geodezyjnej. Podobnie, teodolit i łata niwelacyjna, choć skutecznie współdziałają w pomiarach kątów i różnic wysokości, nie są skonfigurowane do pracy w ramach tachimetrii, która wymaga innego podejścia. Użycie teodolitu i tyczki również prowadzi do nieprawidłowych wyników, ponieważ tyczki służą do zaznaczania punktów w terenie, ale nie mają funkcji pomiarowych, które są kluczowe w tej metodzie. Przy pomiarach geodezyjnych niezwykle istotne jest zrozumienie, że każdy przyrząd geodezyjny ma swoje specyficzne zastosowanie, a ich niewłaściwe łączenie prowadzi do błędów pomiarowych oraz nieefektywności w realizacji projektów budowlanych. Zrozumienie tych różnic jest kluczowe dla uzyskania dokładnych i wiarygodnych wyników w geodezji.

Pytanie 18

Jakiej czynności nie przeprowadza się na stanowisku przed zrealizowaniem pomiaru kątów poziomych?

A. Centrowania teodolitu

B. Regulacji ostrości obrazu

C. Regulacji ostrości krzyża kresek

D. Dokonania pomiaru wysokości teodolitu

Ustawianie ostrości obrazu, ostrości krzyża kresek oraz centrowanie teodolitu to kluczowe czynności, które należy wykonać przed pomiarem kątów poziomych. Wiele osób może myśleć, że pomiar wysokości teodolitu jest równie ważny, co te czynności, jednak zrozumienie ich przeznaczenia jest kluczowe dla prawidłowego wykorzystania instrumentu. Ustawienie ostrości obrazu jest niezbędne, aby uzyskać wyraźny obraz punktu docelowego, co umożliwia dokładne odczytywanie kątów. Ustawienie ostrości krzyża kresek pozwala na precyzyjne wyznaczenie kierunku, co jest niezbędne dla uzyskania wiarygodnych wyników. Centrowanie teodolitu natomiast zapewnia, że punkt pomiarowy znajduje się dokładnie pod osią instrumentu, co jest fundamentalne dla osiągnięcia wysokiej dokładności pomiarów. Nieprawidłowe zrozumienie hierarchii tych czynności prowadzi do błędów pomiarowych, które mogą w konsekwencji wpływać na całą pracę geodezyjną. W praktyce, pomiar wysokości teodolitu jest realizowany w innym kontekście, związanym z pomiarami wysokościowymi, a nie pomiarami kątów poziomych. Dlatego istotne jest, aby przed rozpoczęciem pomiarów kątowych, upewnić się, że wszystkie przygotowania związane z ustawieniem instrumentu są wykonane poprawnie, aby uniknąć błędów i nieprawidłowości.

Pytanie 19

Niwelator to narzędzie służące do dokonania pomiaru

A. kątów zenitalnych

B. różnic wysokości

C. wysokości punktów

D. kątów nachylenia

Niwelator to dosyć specyficzne urządzenie, które służy głównie do mierzenia różnic wysokości pomiędzy punktami w terenie. Jak to działa? Wykorzystuje coś w rodzaju poziomicy, by dokładnie określić te różnice. To bardzo ważne w różnych dziedzinach, takich jak budownictwo czy geodezja, bo dobrze wykonane pomiary wysokości są kluczowe. Na przykład, kiedy budujemy fundamenty, musimy być pewni, że wszystko jest na właściwej wysokości, żeby budowla była stabilna. Niwelatory są też wykorzystywane do tworzenia map topograficznych, gdzie precyzyjne różnice w wysokościach terenu mają ogromne znaczenie. W branży mamy różne normy, jak ISO, które przypominają, jak ważne są dokładne pomiary. A co ciekawe, teraz mamy również niwelatory elektroniczne, które jeszcze bardziej podnoszą jakość pomiarów, co naprawdę ma znaczenie w dzisiejszych projektach budowlanych.

Pytanie 20

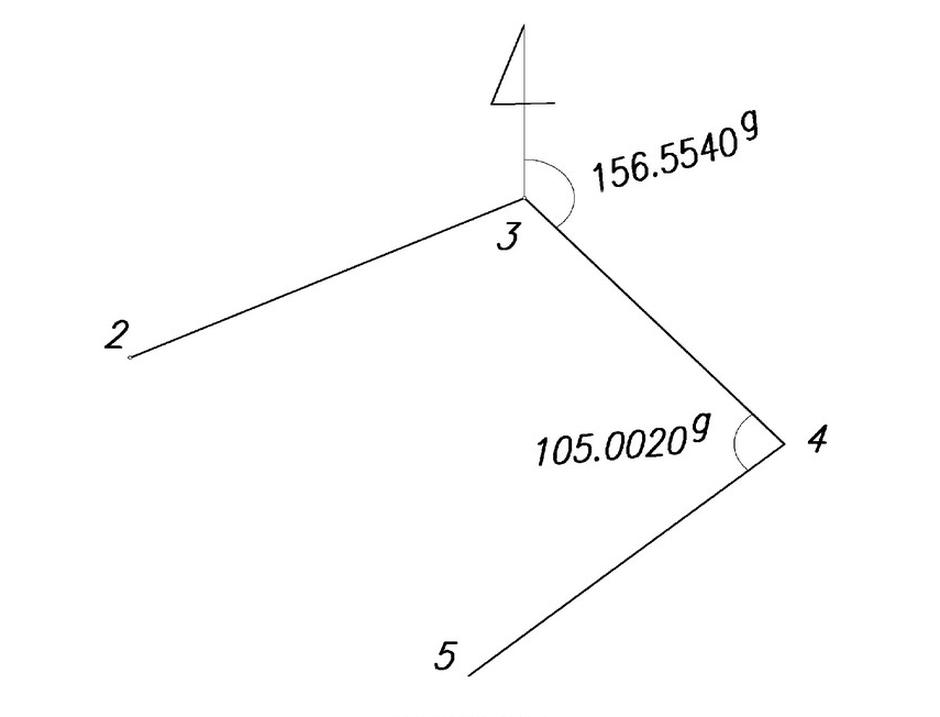
W ciągu poligonowym azymut boku 3-4 równa się 156,5540^g, a kąt "prawy" pomierzony na stanowisku 4 wynosi 105,0020^g. Oblicz azymut boku 4-5.

A. 61,5560g

B. 261,5560g

C. 251,5520g

D. 51,5520g

Azymut boku 4-5 wynosi 251,5520g, co zostało obliczone poprzez dodanie kąta 'prawego' do azymutu boku 3-4. Proces obliczeniowy polega na sumowaniu wartości azymutu i kąta, co jest standardową praktyką w geodezji i inżynierii lądowej. W tym przypadku: 156,5540g (azymut boku 3-4) + 105,0020g (kąt 'prawy') daje nam 261,5560g. Ponieważ uzyskany wynik przekracza 200g, musimy odjąć 200g, co prowadzi do końcowego azymutu 61,5560g. Ta metoda jest fundamentalna w tworzeniu map i pomiarach geodezyjnych, gdzie precyzyjne określenie kierunków jest kluczowe dla dokładności. Przykładowo, w praktyce budowlanej błędne obliczenie azymutu może prowadzić do nieprawidłowego rozmieszczenia fundamentów, co może mieć poważne konsekwencje dla stabilności budynku.

Pytanie 21

Kąty pionowe nachylenia (a) mogą przyjmować wartości +/- w zakresie

A. 0g-300g

B. 0g-200g

C. 0g-100g

D. 0g-400g

Zrozumienie pojęcia kąta nachylenia pionowego jest kluczowe, aby uniknąć nieporozumień w kontekście projektów inżynieryjnych. Odpowiedzi, które sugerują szerszy zakres wartości, takie jak 0°-200°, 0°-300° czy 0°-400°, wskazują na nieprawidłowe podejście do problematyki określania kątów. Kąt nachylenia nie może przekraczać 100°, ponieważ w praktyce każdy kąt powyżej 90° wskazuje na odwrócenie orientacji obiektu, co w przypadku budowli staje się niemożliwe. Przykładowo, kąt 180° oznacza pełne obrócenie obiektu, a wartości powyżej tego są także bez sensu, ponieważ w kontekście rzeczywistych aplikacji inżynieryjnych nie można stosować takich kątów. Wiele osób może mylnie przyjąć, że większe wartości kątów są możliwe, biorąc pod uwagę różne zastosowania lub teoretyczne modele, jednakże praktyczne zastosowanie w inżynierii ogranicza kąt nachylenia do 100°. Należy również pamiętać, że w geodezji i budownictwie bezpieczeństwo oraz stabilność konstrukcji są kluczowe, a zastosowanie nieodpowiednich kątów może prowadzić do niebezpieczeństwa i awarii budynków. Dlatego warto zrozumieć, jakie są zasady i normy w tej dziedzinie, aby podejmować prawidłowe decyzje projektowe.

Pytanie 22

Która z podanych prac geodezyjnych nie wymaga zgłoszenia do Ośrodka Dokumentacji Geodezyjnej i Kartograficznej?

A. Podział działki

B. Pomiar ilości mas ziemnych

C. Zaktualizowanie mapy zasadniczej

D. Inwentaryzacja po zakończeniu budowy

Aktualizacja mapy zasadniczej, inwentaryzacja powykonawcza budynku oraz podział nieruchomości to procesy, które z definicji wiążą się z formalnym zgłaszaniem do Ośrodka Dokumentacji Geodezyjnej i Kartograficznej. Wynika to z ich wpływu na stan prawny oraz dokumentację gruntów. Aktualizacja mapy zasadniczej jest konieczna, gdy zmiany w terenie (np. nowe zabudowy) wymagają odzwierciedlenia w dokumentacji, co ma kluczowe znaczenie dla planowania przestrzennego i zarządzania nieruchomościami. Inwentaryzacja powykonawcza budynku, której celem jest potwierdzenie zgodności wykonanych prac budowlanych z projektem, również musi być zgłoszona, ponieważ zabezpiecza interesy prawne związane z własnością i użytkowaniem obiektów. Podział nieruchomości, z kolei, to proces, który wpływa na prawa własności i również wymaga zgłoszenia, aby zapewnić, że nowe granice są prawidłowo zarejestrowane w dokumentacji geodezyjnej. Dlatego ważne jest, aby zrozumieć, że prace te są nie tylko techniczne, ale również mają istotne konsekwencje prawne i administracyjne, co wymusza ich zgłaszanie do odpowiednich instytucji. Brak zgłoszenia tych prac do ODGiK może prowadzić do nieprawidłowości w księgach wieczystych oraz problemów z uzyskaniem pozwoleń czy realizacją projektów budowlanych.

Pytanie 23

Która z metod niwelacji opiera się na określaniu różnic w wysokości pomiędzy punktami terenu za pomocą zmierzonych kątów pionowych oraz odległości poziomych między tymi punktami?

A. Punktów rozproszonych

B. Reperów

C. Trygonometryczna

D. Geometryczna

Metoda niwelacji trygonometrycznej opiera się na wyznaczaniu różnic wysokości pomiędzy punktami terenowymi przy użyciu pomiarów kątów pionowych oraz odległości poziomych. Ta technika jest szczególnie przydatna w sytuacjach, gdzie bezpośredni dostęp do punktów jest utrudniony lub niemożliwy. W praktyce, inżynierowie często wykorzystują niwelację trygonometryczną do tworzenia bardziej skomplikowanych projektów budowlanych, takich jak mosty czy drogi, gdzie precyzyjne określenie różnic wysokości jest kluczowe. Zastosowanie tej metody pozwala na obliczenia przy użyciu wzorów trygonometrycznych, co zwiększa efektywność pomiarów. Standardy branżowe, takie jak normy ISO dotyczące geodezji, wskazują na niwelację trygonometryczną jako jedną z zalecanych metod w skomplikowanych projektach geodezyjnych, co świadczy o jej uznawanej wartości i praktyczności w dziedzinie inżynierii i geodezji.

Pytanie 24

To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 25

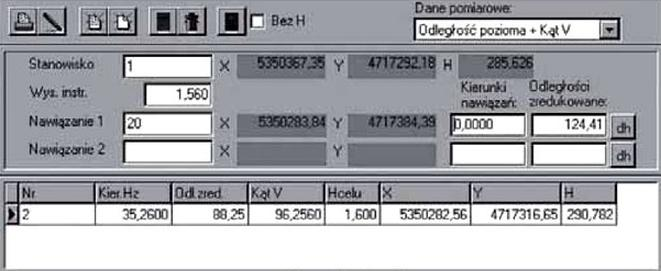
Format zmierzonych i obliczonych wielkości pokazanych na "zrzucie ekranowym" wskazuje, że obliczenia wynikają z pomiaru metodą

A. wcięć.

B. tachimetryczną.

C. prostokątną.

D. biegunową.

Wybór innej metody, takiej jak prostokątna, biegunowa czy wcięć, jest nieprawidłowy z kilku kluczowych powodów. Metoda prostokątna, oparta na współrzędnych prostokątnych, może być stosowana w sytuacjach, gdzie potrzebne są jedynie podstawowe pomiary, jednak nie uwzględnia ona kątów, co czyni ją nieodpowiednią w przypadku analizy danych zawierających kąt horyzontalny oraz pionowy. Z kolei metoda biegunowa, choć również związana z pomiarami kątów, nie dostarcza szczegółowych informacji o odległościach, co jest niezbędne w kontekście doboru sprzętu geodezyjnego, jak taczymetr, który łączy te elementy. Metoda wcięć z kolei skupia się na pomiarach specyficznych dla warunków terenowych, takich jak pomiar głębokości w otworach czy w studniach, co w ogóle nie odnosi się do pomiarów kątów i odległości. Wybór błędnych odpowiedzi często wynika z mylnego założenia, że każda metoda pomiarowa jest uniwersalna. Kluczowe w geodezji jest zrozumienie specyfiki każdej metody oraz umiejętność ich odpowiedniego zastosowania w zależności od wymagań projektu.

Pytanie 26

Korzystając z danych zamieszczonych w tabeli, oblicz kąt skręcenia pomiędzy układami współrzędnych wtórnym i pierwotnym.

Numer punktu	Układ pierwotny		Układ wtórny
	X^p	Y^p	X^w	Y^w
1	100,00	100,00	400,00	400,00
2	123,00	134,00	377,00	366,00
3	145,00	162,00	355,00	338,00
4	200,00	200,00	300,00	300,00

A. 300g

B. 50g

C. 200g

D. 250g

Prawidłowa odpowiedź to 200g, co oznacza kąt skręcenia między układami współrzędnych wtórnym i pierwotnym. Aby obliczyć kąt skręcenia, ważne jest zrozumienie, jak układy współrzędnych są ze sobą powiązane. Kąt ten można określić poprzez analizę różnic między danymi w układzie pierwotnym a tymi w układzie wtórnym. W praktyce, poprawne obliczenie kąta skręcenia jest kluczowe w dziedzinach takich jak inżynieria, architektura oraz robotyka, gdzie precyzyjne określenie orientacji obiektów jest niezbędne do prawidłowego działania mechanizmów i systemów. Kiedy zmieniamy orientację układów współrzędnych, musimy uwzględnić nie tylko kąt, ale także zmiany w lokalizacji oraz ewentualne przekształcenia, które mogą wpłynąć na dalsze obliczenia. Znajomość prawidłowego obliczania kąta skręcenia jest zgodna z najlepszymi praktykami w zakresie projektowania systemów, w których precyzja ma kluczowe znaczenie dla ich funkcjonowania.

Pytanie 27

To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 28

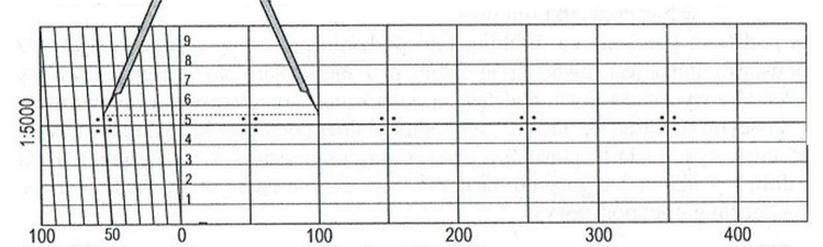
Wartość odczytu, którą wskazuje przestawiona podziałka transwersalna, wynosi

A. 155,5 m

B. 155,0 m

C. 55,0 m

D. 55,5 m

Nieprawidłowe odpowiedzi, takie jak 55,0 m, 55,5 m oraz 155,0 m, wynikają z typowych błędów w interpretacji wartości wskazywanych na podziałce. W wielu przypadkach osoby próbujące odczytać wartość z podziałki nie uwzględniają całkowitego przesunięcia, co prowadzi do błędnych wniosków. Na przykład wybór 55,0 m może wynikać z mylnego założenia, że wartość głównej podziałki jest pomijana i odczytywana jest tylko wartość transwersalna. Z kolei 55,5 m często bywa wynikiem dodania tylko przesunięcia do wartości głównej, bez uwzględnienia odjęcia wartości początkowej, co jest kluczowym krokiem w całym procesie. Odpowiedź 155,0 m również może wynikać z błędnego założenia dotyczącego wartości odjętej, co ilustruje typowe zamieszanie związane z odczytem z podziałek. Aby uniknąć takich pomyłek, istotne jest zrozumienie zasady działania podziałek oraz mechanizmu ich odczytu. Dobrą praktyką jest zawsze przeglądanie kroków obliczeniowych i upewnienie się, że uwzględniamy wszystkie wartości, co jest zgodne z założeniami standardów pomiarowych. Bezpieczne podejście do pomiarów oraz umiejętność ich poprawnej interpretacji jest fundamentem skutecznego działania w dziedzinach związanych z inżynierią i geodezją.

Pytanie 29

W jakiej skali sporządza się mapy zasadnicze dla niewielkich miejscowości, obszarów metropolitalnych i stref przemysłowych?

A. 1 : 500

B. 1 : 1000

C. 1 : 2000

D. 1 : 5000

Odpowiedź 1 : 1000 jest poprawna, ponieważ mapy zasadnicze małych miast, aglomeracji miejskich i obszarów przemysłowych sporządzane są w skali 1 : 1000, co oznacza, że 1 jednostka na mapie odpowiada 1000 jednostkom w rzeczywistości. Przykładowo, jeśli na mapie widoczna jest odległość 1 cm, w rzeczywistości jest to 1000 cm, czyli 10 m. Taka skala pozwala na szczegółowe odwzorowanie urbanistycznych i przestrzennych aspektów obszarów miejskich, co jest niezwykle istotne w planowaniu przestrzennym oraz zarządzaniu infrastrukturą. Przykłady zastosowania obejmują analizy gęstości zabudowy, lokalizację nowych inwestycji, a także ochronę środowiska. Zgodnie z obowiązującymi standardami, mapy zasadnicze powinny być aktualizowane regularnie, aby odzwierciedlały zmiany w zagospodarowaniu przestrzennym, co zwiększa ich użyteczność w praktyce.

Pytanie 30

To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 31

Lokalizacja charakterystycznych punktów w terenie w procesie niwelacji punktów rozprzestrzenionych ustalana jest za pomocą metody

A. tachimetrycznej

B. biegunowej

C. przedłużeń

D. ortogonalnej

Odpowiedzi tachimetryczna, ortogonalna oraz przedłużeń wskazują na różne podejścia w pomiarze i niwelacji, które nie są właściwe w kontekście określenia położenia punktów rozproszonych. Metoda tachimetryczna, choć użyteczna do pomiarów kątów i odległości, nie jest optymalna dla precyzyjnego określania lokalizacji punktów w rozproszonym terenie, ponieważ koncentruje się głównie na pomiarach punktów z jednego stanowiska oraz może prowadzić do błędów w przypadku przeszkód terenowych. Z kolei metoda ortogonalna, która zakłada stosowanie prostokątnych układów współrzędnych, jest bardziej odpowiednia dla zadań, gdzie punkty są poukładane w regularny sposób, a nie w sposób rozproszony. Przedłużenia, w swoim podstawowym sensie, polegają na wydłużaniu linii przez konkretne punkty, co nie odpowiada na potrzeby związane z niwelacją punktów rozproszonych. Wybór niewłaściwej metody może prowadzić do znaczących błędów w pomiarach, co jest szczególnie problematyczne w projektach budowlanych, gdzie precyzja jest kluczowa. Zrozumienie, kiedy i jak stosować konkretne techniki pomiarowe, jest kluczowe dla osiągnięcia sukcesu w obszarze geodezji i inżynierii lądowej.

Pytanie 32

To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 33

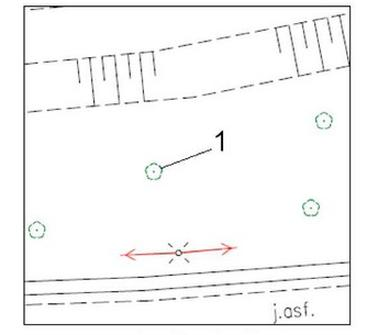
Na fragmencie mapy cyfrą 1 oznaczono

A. zakrzewienie.

B. drzewo iglaste.

C. drzewo liściaste.

D. zadrzewienie.

Odpowiedź "drzewo liściaste" jest poprawna, ponieważ symbol oznaczający cyfrą 1 na przedstawionym fragmencie mapy jest zgodny z konwencjami stosowanymi w mapach topograficznych w Polsce. Drzewa liściaste, takie jak dęby, buki czy klony, są reprezentowane przez charakterystyczne symbole graficzne, które różnią się od symboli stosowanych dla drzew iglastych. Zrozumienie legendy mapy jest kluczowe dla poprawnej interpretacji przedstawionych informacji. W praktyce, wiedza o tym, jak odczytywać symbole na mapach, jest niezbędna dla geodetów, planistów i ekologów, którzy często korzystają z map w swojej pracy. Znajomość różnic między rodzajami drzew jest również istotna przy podejmowaniu decyzji o sadzeniu roślin, ponieważ różne gatunki mają różne wymagania środowiskowe oraz wpływają na bioróżnorodność regionu. Dlatego znajomość symboli kartograficznych nie tylko ułatwia nawigację, ale również wspiera podejmowanie bardziej świadomych decyzji w zakresie zarządzania przestrzenią.

Pytanie 34

To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 35

Która z wielkości jest obciążona błędem indeksu w trakcie pomiaru?

A. Kierunek poziomy

B. Odczyt na łacie

C. Kierunek pionowy

D. Odległość skośna

Kierunek pionowy może być trudny, bo trzeba uważać na różne rzeczy, jak na przykład grawitacja. Jak mierzysz, to ważne jest, żeby instrument był dobrze ustawiony, bo inaczej wychodzą błędy. Myślę, że w geodezji, szczególnie przy mierzeniu wysokości budynków czy terenów, każdy mały błąd w kierunku pionowym potrafi narobić dużych problemów. Dlatego geodeci powinni regularnie kalibrować swoje sprzęty i sprawdzać, czy są właściwie ustawione. Na przykład, korzystając z teodolitów czy niwelatorów, powinni brać pod uwagę warunki atmosferyczne, bo one potrafią wpłynąć na wyniki. Kluczowe jest zrozumienie tych rzeczy, bo to pozwala uzyskać dokładne pomiary, a to jest bardzo ważne w naszej działce.

Pytanie 36

Który z rysunków przedstawia określenie współrzędnych punktu wcinanego za pomocą kątowego wcięcia w przód?

A. D.

B. A.

C. B.

D. C.

Wybór innej odpowiedzi może wynikać z niepełnego zrozumienia koncepcji określenia współrzędnych punktu wcinanego za pomocą kątowego wcięcia w przód. Wiele osób ma tendencję do myślenia, że każda kombinacja linii i kątów może prowadzić do poprawnego określenia punktu, co jest błędnym założeniem. Na przykład, rysunki A, B i D mogą przedstawiać różne układy geometryczne, które nie spełniają kluczowego warunku, jakim jest właściwe ustawienie kątów α i β. Często błędne koncepcje wynikają z mylenia pojęć związanych z kątami i ich interpretacją w kontekście współrzędnych. W wielu przypadkach, wybierając nieodpowiedni rysunek, można dojść do przekonania, że jedynie obecność linii i kątów jest wystarczająca do określenia punktu, co jest nieprawidłowe. W rzeczywistości, aby uzyskać dokładne współrzędne, konieczne jest spełnienie specyficznych warunków geometrycznych, które uwzględniają nie tylko obecność kątów, ale także ich odpowiednie ustawienie względem siebie. Niekiedy również brakuje zrozumienia, jak istotne jest użycie standardów branżowych przy określaniu współrzędnych w projektach inżynieryjnych. Dlatego ważne jest, aby uczyć się i stosować poprawne metody geometryczne zgodne z najlepszymi praktykami, co pozwala na uniknięcie błędów przy projektowaniu i realizacji zadań technicznych.

Pytanie 37

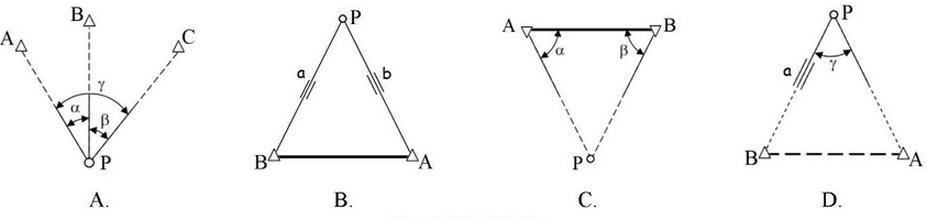
Jaką wartość ma kąt, o który trzeba obrócić alidadę przy precyzyjnym poziomowaniu teodolitu, po ustawieniu libelli równolegle do osi dwóch śrub regulacyjnych oraz ustawieniu pęcherzyka w pozycji centralnej?

A. 360°

B. 180°

C. 200°

D. 90°

Odpowiedź 90° jest poprawna, ponieważ podczas dokładnego poziomowania teodolitu, alidade musi być obrócona o kąt prosty względem linii ustawczych, aby uzyskać odpowiednią orientację. Obrót o 90° umożliwia precyzyjne sprawdzenie poziomu w kierunku prostopadłym do linii, na której zainstalowano teodolit. W praktyce, obrócenie alidade o ten kąt umożliwia wykonanie pomiarów w dwóch prostopadłych kierunkach, co jest istotne dla uzyskania dokładnych wyników. W standardach branżowych, takich jak normy ISO dotyczące pomiarów geodezyjnych, wskazuje się na znaczenie precyzyjnego poziomowania i wykorzystania alidady do potwierdzenia poprawności ustawienia urządzenia. W przypadku pomiarów budowlanych lub inżynieryjnych, prawidłowe poziomowanie teodolitu jest kluczowe, aby uniknąć błędów, które mogą prowadzić do kosztownych poprawek i opóźnień. Dlatego znajomość technik obrotu alidade oraz ich zastosowanie w praktyce jest niezbędna dla każdego geodety.

Pytanie 38

Podczas opracowania mapy zasadniczej przy użyciu oprogramowania kartograficznego punkty osnowy geodezyjnej zostaną domyślnie opisane czcionką o rozmiarze

A. 2,0 mm

B. 1,0 mm

C. 2,5 mm

D. 1,8 mm

Odpowiedź 1,8 mm jest prawidłowa, ponieważ w większości nowoczesnych programów kartograficznych, takich jak QGIS czy ArcGIS, domyślny rozmiar czcionki dla opisu punktów osnowy geodezyjnej wynosi właśnie 1,8 mm. Wybór odpowiedniego rozmiaru czcionki jest kluczowy dla czytelności mapy, szczególnie w kontekście dostosowania do wymogów standardów kartograficznych takich jak norma ISO 19117 dotycząca wizualizacji informacji geograficznej. Użycie 1,8 mm zapewnia odpowiednią widoczność opisów, co jest niezbędne w pracy geodetów i kartografów, którzy muszą precyzyjnie przekazywać informacje na mapach. Na przykład, w przypadku tworzenia map zasadniczych, które są wykorzystywane do celów prawnych lub administracyjnych, czytelność i dokładność opisu punktów osnowy geodezyjnej mają kluczowe znaczenie. Warto również zwrócić uwagę, że w różnych typach map, w zależności od skali, wielkość czcionki może być dostosowywana, ale 1,8 mm stanowi powszechną praktykę w wielu sytuacjach kartograficznych.

Pytanie 39

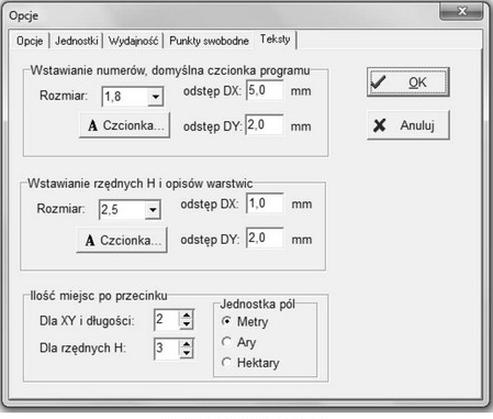
To pytanie jest dostępne tylko dla zalogowanych użytkowników. Zaloguj się lub utwórz konto aby zobaczyć pełną treść pytania.

Odpowiedzi dostępne po zalogowaniu.

Wyjaśnienie dostępne po zalogowaniu.

Pytanie 40

W niwelacji trygonometrycznej przewyższeniem określamy różnicę wysokości między

A. sąsiednimi reperami

B. punktem celowania a stanowiskiem instrumentu

C. reperami a punktem celowania

D. punktem celowania a horyzontem instrumentu

Przewyższenie w niwelacji trygonometrycznej to kluczowy element w procesie pomiarów geodezyjnych, odnoszący się do różnicy wysokości pomiędzy punktem celowania a horyzontem instrumentu. Oznacza to, że aby poprawnie określić różnice wysokości na danym terenie, geodeta musi zrozumieć, jak działa instrument niwelacyjny. Horyzont instrumentu jest poziomą linią, która służy jako odniesienie do pomiarów, a punkt celowania to punkt, w który kieruje się niwelator. Praktyczne zastosowanie tej wiedzy można zobaczyć w projektach budowlanych, infrastrukturze drogowej oraz w geodezyjnych pomiarach terenowych. Prawidłowe określenie przewyższenia jest kluczowe dla zapewnienia, że konstrukcje będą zgodne z wymaganiami projektowymi, a także w celu uniknięcia błędów, które mogłyby prowadzić do problemów w przyszłości. W geodezji stosuje się standardy takie jak normy PN-EN 2878, które wskazują na metodyki pomiarów i interpretacji wyników, co jest istotne w kontekście precyzyjnych prac geodezyjnych oraz inżynieryjnych.

Rozpocznij nowy egzamin

Powrót do strony głównej