Wyniki egzaminu

Nowy egzamin

Informacje o egzaminie:

Zawód: Technik geodeta
Kwalifikacja: BUD.18 - Wykonywanie pomiarów sytuacyjnych, wysokościowych i realizacyjnych oraz opracowywanie wyników tych pomiarów
Data rozpoczęcia: 16 lutego 2026 13:51
Data zakończenia: 16 lutego 2026 14:05

Egzamin zdany!

Wynik: 27/40 punktów (67,5%)

Wymagane minimum: 20 punktów (50%)

Pochwal się swoim wynikiem!

Facebook

X.com

Szczegółowe wyniki:

Pytanie 1

Jakiego z wymienionych przyrządów należy użyć do pomiaru przemieszczeń w kierunku pionowym przęseł mostu?

A. Tensometru

B. Pionownika

C. Niwelatora

D. Inklinometru

Wybór instrumentu do pomiaru przemieszczeń pionowych przęseł mostu jest kluczowy dla zapewnienia stabilności i bezpieczeństwa takiej konstrukcji. Tensometr, jako urządzenie do pomiaru odkształceń materiałów, koncentruje się na analizie naprężeń i deformacji, a nie na bezpośrednim pomiarze przemieszczeń pionowych. Zastosowanie tensometru w tej sytuacji mogłoby prowadzić do nieprecyzyjnych wniosków, ponieważ nie uwzględnia on ogólnych zmian wysokości konstrukcji. Pionownik, z kolei, służy do ustalania pionowości obiektów i nie jest narzędziem do pomiaru przemieszczeń, co również czyni go nieodpowiednim w kontekście pomiarów mostowych. Inklinometr, mimo że jest użyteczny w monitorowaniu kątów nachylenia, nie jest dedykowany do pomiarów poziomych przemieszczeń, co ogranicza jego zastosowanie w kontekście pomiarów przęseł mostowych. W praktyce, wybór niewłaściwego instrumentu do monitorowania przemieszczeń mógłby prowadzić do niewłaściwej oceny kondycji mostu i potencjalnych zagrożeń. W związku z tym, kluczowym jest, aby odpowiednio dobierać narzędzia pomiarowe, zgodnie z ich przeznaczeniem i funkcjonalnością, co zapewnia bezpieczeństwo i niezawodność konstrukcji inżynieryjnych.

Pytanie 2

Jakie jest przybliżone znaczenie błędu względnego dla odcinka o długości 500,00 m, który został zmierzony z błędem średnim ±10 cm?

A. 1/500

B. 1/1000

C. 1/2000

D. 1/5000

Błąd względny jest miarą precyzji pomiaru, wyrażoną jako stosunek błędu bezwzględnego do wartości rzeczywistej. W tym przypadku długość odcinka wynosi 500,00 m, a błąd pomiarowy wynosi ±10 cm, co odpowiada 0,1 m. Aby obliczyć błąd względny, należy podzielić błąd bezwzględny przez wartość rzeczywistą: 0,1 m / 500 m = 0,0002. To daje 0,0002, co w postaci ułamka jest równe 1/5000. Takie obliczenia są niezwykle istotne w inżynierii oraz metrologii, gdzie precyzja pomiarów ma kluczowe znaczenie. Na przykład w budownictwie, gdzie dokładne pomiary długości mogą wpłynąć na bezpieczeństwo konstrukcji. Właściwe obliczenie błędu względnego pozwala na ocenę jakości użytych narzędzi pomiarowych oraz metod, a także na identyfikację obszarów, w których można poprawić dokładność pomiarów. Przykładem mogą być zastosowania w geodezji, gdzie precyzyjnie określone granice działek są niezbędne do prawidłowego podziału gruntów.

Pytanie 3

Jaką odległość mają punkty hektometrowe na osi trasy?

A. 100 m

B. 150 m

C. 200 m

D. 50 m

Wybierając odpowiedzi inne niż 100 m, można wprowadzić się w błąd co do podstawowych zasad pomiarowych w kontekście tras i punktów odniesienia. Odpowiedź wskazująca na 50 m nie tylko ignoruje fakt, że punkty hektometrowe są definiowane jako oddalone o 100 m, ale także sugeruje, że mogłyby być one stosowane w sytuacjach, gdzie precyzyjna lokalizacja nie jest kluczowa. To zaburza zrozumienie koncepcji dystansu w kontekście tras transportowych. Odpowiedź 150 m również jest myląca, ponieważ nie odzwierciedla rzeczywistych standardów pomiarowych, które uwzględniają jedynie jednostki metrów w wielokrotności setek. Natomiast 200 m wskazuje na znaczny błąd, gdyż wydłuża odległość między punktami, co może prowadzić do problemów w zarządzaniu ruchem i lokalizacji obiektów. W praktyce, używanie błędnych odległości może skutkować niewłaściwym planowaniem tras i zwiększoną nieefektywnością w operacjach logistycznych. Zrozumienie poprawnych jednostek miary i ich zastosowania jest niezbędne do prawidłowego funkcjonowania w branży transportowej, a także do unikania typowych błędów myślowych, które mogą zniekształcić rzeczywisty obraz sytuacji na trasie.

Pytanie 4

Jeśli pomiar na łacie niwelacyjnej w kierunku wstecznym wyniósł 3549, a na łacie w kierunku przednim 0506, jaka jest różnica wysokości na pozycji niwelatora?

A. -4,055 m

B. +3,043 m

C. +4,055 m

D. -3,043 m

Odpowiedź +3,043 m jest poprawna, ponieważ obliczenie różnicy wysokości na stanowisku niwelatora opiera się na zasadzie, że różnica ta jest równa odczytowi na łacie wstecz minus odczytowi na łacie w przód. W tym przypadku, mamy 3549 mm (odczyt wstecz) minus 0506 mm (odczyt w przód). Wykonując to obliczenie: 3549 - 506 = 3043 mm. Przekształcając milimetry na metry, otrzymujemy 3,043 m, co oznacza, że niwelator znajdował się na wyższej wysokości względem łaty w przód. W praktyce, takie obliczenia są kluczowe w geodezji i budownictwie, gdyż pozwalają na precyzyjne ustalanie różnic wysokości, co jest niezbędne przy wyznaczaniu poziomów budynków, dróg czy innych konstrukcji. Zgodnie z zaleceniami branżowymi, ważne jest również, aby przed przystąpieniem do pomiarów sprawdzić kalibrację sprzętu, aby zapewnić dokładność wyników pomiarów.

Pytanie 5

W trakcie projektowania osnów geodezyjnych nie przeprowadza się

A. stabilizacji punktów geodezyjnych

B. wywiadu z terenu

C. inwentaryzacji już istniejących punktów geodezyjnych

D. ustalenia lokalizacji i zabudowy poszczególnych punktów sieci

Stabilizacja punktów geodezyjnych to coś, co dzieje się dopiero po tym, jak mamy już zaplanowaną sieć punktów. Najpierw trzeba wybrać dobre miejsca i odpowiednio je rozmieścić. W tym etapie ważne jest, żeby dokładnie sprawdzić, jakie punkty już są w terenie, porozmawiać z ludźmi, którzy tam byli i ustalić, w jakich miejscach najlepiej postawić nowe punkty. To wszystko pomoże nam zrobić sieć, która będzie zgodna z normami i potrzebami. Stabilizacja przychodzi dopiero, gdy mamy już pewność, gdzie mają być te punkty. Na przykład, kiedy projekt jest gotowy, przystępuje się do ich stabilizacji, co oznacza, że umieszczamy je w terenie i dobrze zabezpieczamy. Warto pamiętać, że stabilizacja musi być przeprowadzona zgodnie z obowiązującymi normami, jak chociażby PN-EN ISO 17123, żeby wyniki były rzetelne i miały dobrą jakość.

Pytanie 6

Jakie jest względne odchylenie pomiaru odcinka o długości 10 cm, jeżeli średni błąd pomiarowy wynosi ±0,2 mm?

A. 1:100

B. 1:50

C. 1:500

D. 1:200

Podczas analizy błędów względnych, istotne jest zrozumienie, że nie każdy błąd jest bezpośrednio proporcjonalny do wielkości mierzonych. W przypadku błędnych odpowiedzi, które sugerują inne proporcje, istnieje pewne niezrozumienie podstaw metrologii i obliczeń. Na przykład, jeśli ktoś wybrał proporcję 1:100, może to wynikać z koncentracji na błędzie bezwzględnym bez odniesienia go do wartości rzeczywistej. W rzeczywistości, przy długości 10 cm, błąd ±0,2 mm jest stosunkowo niewielki, co prowadzi do niższego współczynnika błędu względnego, niż sugeruje ta odpowiedź. Odpowiedzi 1:200 i 1:50 również nie uwzględniają poprawnych przeliczeń, ponieważ błąd bezwzględny jest zbyt mały w porównaniu do wartości mierzonych, co wskazuje na zbyt dużą tolerancję na błędy. Warto również zauważyć, że w kontekście nauk przyrodniczych i inżynieryjnych, stosowanie błędów względnych jest kluczowe do oceny jakości danych. Często, pomijając obliczenia błędów względnych, można wprowadzić nieporozumienia dotyczące precyzji i niezawodności pomiarów. Dlatego tak ważne jest, aby przy obliczeniach błędów zawsze odnosić je do wartości rzeczywistej, aby uzyskać miarodajne wyniki.

Pytanie 7

Teoretyczna suma kątów wewnętrznych zamkniętego pięcioboku wynosi

A. 800g

B. 400g

C. 600g

D. 1000g

Suma teoretyczna kątów wewnętrznych wielokąta obliczana jest za pomocą wzoru: (n - 2) × 180°, gdzie n jest liczbą boków wielokąta. Dla pięcioboku, n wynosi 5, więc suma kątów wynosi (5 - 2) × 180° = 3 × 180° = 540°. Zwróć uwagę, że w tym pytaniu chodzi o pięciobok zamknięty, co jest istotne, ponieważ w kontekście geometrii zamkniętej suma kątów wewnętrznych zawsze pozostaje stała i wynosi właśnie 540°. W praktyce, znajomość sumy kątów wewnętrznych jest kluczowa w architekturze i inżynierii, gdzie obliczenia dotyczące kształtów i konstrukcji budynków oraz innych obiektów są niezbędne. Na przykład, projektując dachy wielokątne, architekci muszą uwzględniać tę wartość, aby zapewnić prawidłowe wymiary i estetykę budynku. Wartości kątów są również istotne przy tworzeniu modeli 3D, gdzie dokładność geometrii ma bezpośrednie przełożenie na jakość wizualizacji i obliczeń fizycznych.

Pytanie 8

Wysokość osi celowej to 213,100 m. Na jakim pomiarze powinna być umieszczona łatę, aby osiągnięta wysokość punktu wyniosła 212,800?

A. 1300 mm

B. 0030 mm

C. 0300 mm

D. 3000 mm

Aby obliczyć, na jakim odczycie należy ustawić łatę, aby wysokość realizowanego punktu wyniosła 212,800 m, musimy skorzystać z pojęcia różnicy wysokości. Wysokość osi celowej wynosi 213,100 m, a zatem różnica między wysokością osi celowej a wysokością punktu wynosi 213,100 m - 212,800 m = 0,300 m, co jest równoważne 300 mm. Oznacza to, że aby uzyskać żądaną wysokość, musimy ustawić łatę na odczycie 300 mm. W praktyce, przy pomiarach geodezyjnych, stosuje się ten typ obliczeń w celu precyzyjnego ustalenia poziomu obiektów budowlanych lub innych punktów odniesienia. Tego rodzaju obliczenia są kluczowe w geodezji i budownictwie, gdzie precyzyjne pomiary wysokościowe są niezbędne do zapewnienia stabilności i poprawności konstrukcji budowlanych.

Pytanie 9

Jakie jest zwiększenie współrzędnej ∆y_1-2, jeśli zmierzona długość d_1-2 = 100,00 m, a sinA_1-2 = 0,8910 oraz cosA_1-2 = 0,4540?

A. 89,10 m

B. 8,91 m

C. 45,40 m

D. 4,54 m

Wybór odpowiedzi innych niż 89,10 m wskazuje na nieporozumienie dotyczące zastosowania funkcji trygonometrycznych w kontekście pomiarów i obliczeń. Na przykład, odpowiedzi wskazujące wartości takie jak 8,91 m, 45,40 m czy 4,54 m są wynikiem błędnych interpretacji wzoru na przyrost współrzędnej. Często zdarza się, że osoby, które nie mają solidnych podstaw w trygonometrii, mogą mylić wartości sinusoidalne z innymi parametrami, co prowadzi do błędnych obliczeń. Zastosowanie funkcji sinusowego w obliczeniach jest kluczowe, ponieważ to właśnie dzięki niemu jesteśmy w stanie określić wysokość w oparciu o długość oraz kąt. Odpowiedzi 8,91 m i 4,54 m mogą sugerować błędne pomnożenie lub podział, natomiast 45,40 m może wynikać z niepoprawnego zastosowania wartości cosinus, co nie ma zastosowania w tym kontekście. Kluczowe jest zrozumienie, że do obliczenia przyrostu wysokości (∆y) potrzebujemy wartości sinus, a nie cosinus, co jest fundamentalnym błędem w myśleniu matematycznym. W praktyce, niepoprawne obliczenia mogą prowadzić do poważnych konsekwencji w inżynierii i architekturze, gdzie precyzja jest niezbędna, a nieprawidłowe dane mogą skutkować niewłaściwym zaprojektowaniem konstrukcji lub systemów nawigacyjnych.

Pytanie 10

Która z wielkości jest obciążona błędem indeksu w trakcie pomiaru?

A. Kierunek poziomy

B. Odległość skośna

C. Odczyt na łacie

D. Kierunek pionowy

Kierunek pionowy może być trudny, bo trzeba uważać na różne rzeczy, jak na przykład grawitacja. Jak mierzysz, to ważne jest, żeby instrument był dobrze ustawiony, bo inaczej wychodzą błędy. Myślę, że w geodezji, szczególnie przy mierzeniu wysokości budynków czy terenów, każdy mały błąd w kierunku pionowym potrafi narobić dużych problemów. Dlatego geodeci powinni regularnie kalibrować swoje sprzęty i sprawdzać, czy są właściwie ustawione. Na przykład, korzystając z teodolitów czy niwelatorów, powinni brać pod uwagę warunki atmosferyczne, bo one potrafią wpłynąć na wyniki. Kluczowe jest zrozumienie tych rzeczy, bo to pozwala uzyskać dokładne pomiary, a to jest bardzo ważne w naszej działce.

Pytanie 11

Na precyzję pomiarów niwelacyjnych nie wpływa

A. odległość między niwelatorem a łatami

B. kolejność dokonywanych pomiarów

C. wyważenie łat niwelacyjnych

D. poziomowanie libelli niwelacyjnej

Kolejność wykonywanych odczytów w niwelacji nie ma wpływu na dokładność pomiarów, ponieważ kluczowe są inne aspekty techniczne, takie jak poziomowanie i spionizowanie instrumentu oraz prawidłowe ustawienie łat. W praktyce niwelacyjnym, jeżeli wszystkie pomiary są wykonywane zgodnie z wymaganiami i standardami, to niezależnie od kolejności odczytów wynik końcowy będzie taki sam, pod warunkiem, że nie popełniono błędów w innych etapach procesu. Standardy takie jak PN-EN 17123-1:2018 określają procedury, które minimalizują błędy pomiarowe. Przykładowo, jeżeli niwelator jest starannie spoziomowany, a łatka jest poprawnie ustawiona w pionie, uzyskane wyniki będą wiarygodne niezależnie od tego, w jakiej kolejności zrealizujemy pomiary. To podejście może być stosowane w różnych projektach budowlanych i inżynieryjnych, co podkreśla znaczenie rzetelności technicznej nad subiektywną interpretacją kolejności działań.

Pytanie 12

Które z przedstawionych na rysunku punktów są punktami głównymi łuku kołowego, będącego elementem trasy drogowej?

A. W, H, O

B. S, H, O

C. P, H, K

D. P, S, K

Odpowiedź P, S, K jest prawidłowa, ponieważ punkty te są kluczowymi elementami łuku kołowego w geometrii drogowej. Punkt początkowy (P) reprezentuje miejsce, w którym łuk się zaczyna, co jest istotne dla prawidłowego projektowania trasy, a także dla zapewnienia bezpieczeństwa i komfortu jazdy. Punkt styczności (S) to miejsce, w którym pojazd przechodzi z odcinka prostego na łuk, co ma znaczenie przy projektowaniu przejść między różnymi typami nawierzchni oraz przy obliczaniu promieni łuków, które wpływają na prędkość oraz stabilność ruchu. Punkt końcowy (K) wyznacza zakończenie łuku, co jest istotne dla dalszego prowadzenia trasy i jej planowania. W praktyce, poprawne zrozumienie i zastosowanie tych punktów jest kluczowe, aby zapewnić zgodność z normami projektowania dróg, takimi jak PN-EN 1991, które regulują parametry geometrii drogi oraz wpływają na bezpieczeństwo użytkowników dróg.

Pytanie 13

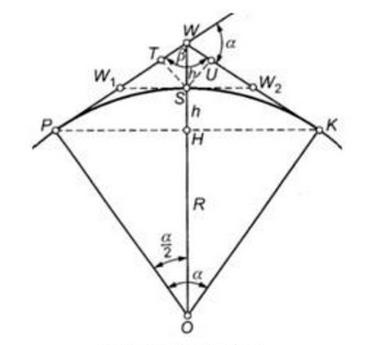
Oblicz wysokość H punktu C w oparciu o dane zapisane na rysunku i w tabeli.

A. HC = 1053,42 m

B. HC = 203,79 m

C. HC = 306,51 m

D. HC = 203,95 m

Obliczenie wysokości punktu C na poziomie 203,95 m jest poprawne, ponieważ opiera się na precyzyjnych danych pomiarowych oraz właściwej interpretacji kątów i poziomów odniesienia zawartych w tabeli. W praktyce, przy pomiarach geodezyjnych, istotne jest zachowanie odpowiednich standardów, takich jak normy PN-EN ISO 17123, które dotyczą metod pomiarów wysokości. Wykorzystanie sprzętu takiego jak niwelatory czy tachymetry, które umożliwiają dokładne pomiary, jest kluczowe. Przykładem zastosowania tej wiedzy jest realizacja projektów budowlanych, gdzie precyzyjne ustalenie wysokości punktów odniesienia ma kluczowe znaczenie dla stabilności konstrukcji. W kontekście geodezji, sposób obliczeń oraz dbałość o poprawność danych wejściowych ma kluczowe znaczenie, aby unikać błędów, które mogą prowadzić do kosztownych konsekwencji. Zrozumienie zasadności wyników oraz ich praktycznego zastosowania w pracy geodezyjnej jest fundamentem dla każdego specjalisty w tej dziedzinie.

Pytanie 14

Na podstawie wzoru przedstawionego w ramce oblicz błąd centrowania podczas tyczenia punktu metodą biegunową, jeżeli długość domiaru wynosi 100 m, a długość celowej odniesienia 400 m.

Błąd centrowania instrumentu:
$$0,7 \times \frac{L}{c} \times m_e$$
gdzie:
$ L $ - długość domiaru
$ c $ - długość celowej odniesienia
$ m_e $ - mianownik skali mapy = 2 mm

A. 0,40 mm

B. 0,35 mm

C. 3,50 mm

D. 4,00 mm

Wybór odpowiedzi, które nie są zgodne z właściwym wynikiem 0,35 mm, jest wynikiem niepełnego zrozumienia wzoru na błąd centrowania. Wiele osób mogło skoncentrować się na nieprawidłowym podstawieniu wartości do wzoru lub na nieprawidłowym zastosowaniu jednostek. Na przykład, niektórzy mogą myśleć, że błąd centrowania można obliczyć bez uwzględnienia mimośrodu stanowiska (me), co jest fundamentalnym błędem w geodezji. Mimośród jest kluczowym elementem, który wpływa na dokładność pomiarów. Ignorowanie tego czynnika prowadzi do nieprawidłowych wyników, które mogą być mylące. Dodatkowo, w przypadku błędnych odpowiedzi, takich jak 0,40 mm czy 4,00 mm, możliwe jest, że osoby udzielające takich odpowiedzi myliły się w stosunku do skali, na której prowadziły obliczenia, lub niepoprawnie interpretowały wartości domiaru oraz celowej odniesienia. Obliczenia centrowania są niezwykle istotne dla zapewnienia precyzyjnych wyników w projektach budowlanych oraz pomiarowych. Również, przy ocenie błędów, niezbędne jest zrozumienie, że każde niewłaściwe założenie może prowadzić do późniejszych konsekwencji w realizacji projektów inżynieryjnych, dlatego tak istotne jest dogłębne zrozumienie oraz poprawne stosowanie wzorów w praktyce.

Pytanie 15

Na mapie w skali 1:2000 zmierzono odcinek o długości 145,4 mm. Jakiemu odcinkowi w rzeczywistości odpowiada ta długość?

A. 14,54 m

B. 290,80 m

C. 145,40 m

D. 29,08 m

Błędne odpowiedzi wynikają z nieprawidłowego zrozumienia przeliczenia skali mapy. Często spotykanym błędem jest mylenie jednostek miary lub nieprawidłowe mnożenie przez współczynnik skali. Na przykład odpowiedź 145,40 m sugeruje, że użytkownik pomnożył długość odcinka na mapie przez 1, co jest całkowicie błędne. Ponadto, gdy ktoś odpowiada 29,08 m, może to sugerować, że podzielił długość odcinka przez 10, co również nie ma sensu w kontekście skali. Odpowiedź 14,54 m może wynikać ze zrozumienia, że najpierw przeliczono jednostki na centymetry, a następnie podzielono przez 100, co jest nieprawidłowym podejściem. Typowe błędy myślowe w takich przypadkach wynikają z nieznajomości zasad przeliczania jednostek czy też błędnego założenia o proporcjach. Aby uniknąć tych pułapek, ważne jest, aby zawsze pamiętać o zasadzie, że w przypadku skali, wartości są mnożone, a nie dzielone. Zrozumienie tych zasad jest kluczowe nie tylko w kontekście nauki o geodezji, ale również w wielu innych dziedzinach, jak architektura czy inżynieria lądowa.

Pytanie 16

Jaką wartość ma kąt, o który trzeba obrócić alidadę przy precyzyjnym poziomowaniu teodolitu, po ustawieniu libelli równolegle do osi dwóch śrub regulacyjnych oraz ustawieniu pęcherzyka w pozycji centralnej?

A. 200°

B. 360°

C. 90°

D. 180°

Obroty o 180°, 360° lub 200° są błędne, ponieważ nie są one zgodne z zasadami dokładnego poziomowania teodolitu. Obrót o 180° oznaczałby, że alidade byłaby ustawiona w przeciwnym kierunku, co nie pozwoliłoby na właściwe sprawdzenie poziomowania w kierunkach prostopadłych. Taki kąt nie przynosi dodatkowych informacji o poziomie, a jedynie przesuwa punkt odniesienia na linię, co jest niepraktyczne w kontekście precyzyjnych pomiarów. Obrót o 360° oznaczałby, że alidade powróciłaby do pierwotnej pozycji, co również jest nieefektywne, gdyż nie wprowadza żadnych nowych danych dotyczących poziomowania. Natomiast wybór 200° jest nieadekwatny, gdyż nie ma uzasadnienia geodezyjnego dla takiego kąta w kontekście wykonywania pomiarów z wykorzystaniem teodolitu. W geodezji, każdy kąt obrotu i jego zastosowanie powinny być dobrze przemyślane i oparte na standardach, które gwarantują dokładność i niezawodność pomiarów. Użytkownicy teodolitu muszą być świadomi, że niepoprawne podejście do poziomowania prowadzi do błędnych wyników, które mogą skutkować poważnymi konsekwencjami w projektach budowlanych i inżynieryjnych.

Pytanie 17

W ciągu poligonowym azymut boku 3-4 równa się 156,5540^g, a kąt "prawy" pomierzony na stanowisku 4 wynosi 105,0020^g. Oblicz azymut boku 4-5.

A. 251,5520g

B. 61,5560g

C. 261,5560g

D. 51,5520g

Azymut boku 4-5 wynosi 251,5520g, co zostało obliczone poprzez dodanie kąta 'prawego' do azymutu boku 3-4. Proces obliczeniowy polega na sumowaniu wartości azymutu i kąta, co jest standardową praktyką w geodezji i inżynierii lądowej. W tym przypadku: 156,5540g (azymut boku 3-4) + 105,0020g (kąt 'prawy') daje nam 261,5560g. Ponieważ uzyskany wynik przekracza 200g, musimy odjąć 200g, co prowadzi do końcowego azymutu 61,5560g. Ta metoda jest fundamentalna w tworzeniu map i pomiarach geodezyjnych, gdzie precyzyjne określenie kierunków jest kluczowe dla dokładności. Przykładowo, w praktyce budowlanej błędne obliczenie azymutu może prowadzić do nieprawidłowego rozmieszczenia fundamentów, co może mieć poważne konsekwencje dla stabilności budynku.

Pytanie 18

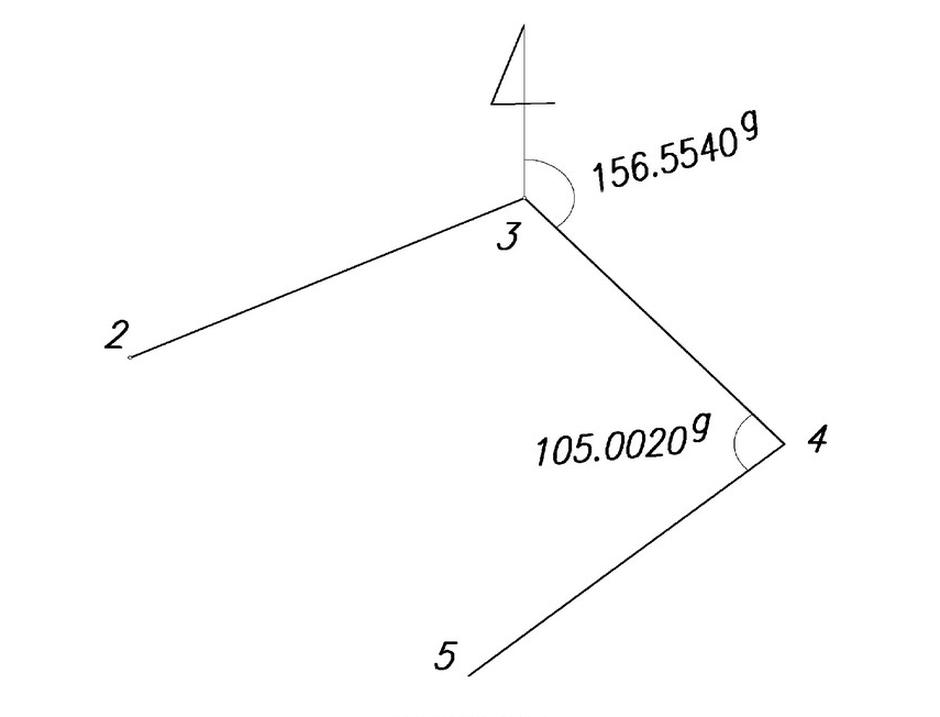
Którą dokładność określenia powierzchni ustawiono dla nowo zakładanego projektu na przedstawionym obrazie okna dialogowego programu geodezyjnego?

A. 1 a

B. 1 dm2

C. 1 m2

D. 1 ha

Odpowiedź "1 m2" jest prawidłowa, ponieważ w kontekście geodezyjnym dokładność określenia powierzchni z wartością 4 oznacza precyzyjność do jednego metra kwadratowego. W praktyce oznacza to, że w przypadku pomiarów geodezyjnych, takich jak wyznaczanie granic działek czy obliczanie powierzchni terenów, możemy spodziewać się, że nasza pomiarowa powierzchnia będzie mieściła się w granicach 1 m2. Ustawienie tej dokładności jest zgodne z normami geodezyjnymi, które wymagają, aby podczas projektowania i wykonywania pomiarów przestrzennych stosować odpowiednie standardy, co zapewnia rzetelność i wiarygodność wyników. W przypadku większych projektów, takich jak planowanie urbanistyczne czy inżynieryjne, znajomość jednostek miary oraz umiejętność właściwego ich zastosowania jest kluczowa dla uzyskania wiarygodnych wyników. Warto również pamiętać, że różne rodzaje działań geodezyjnych mogą wymagać różnych standardów dokładności, dlatego elastyczność w podejściu do pomiarów jest istotna.

Pytanie 19

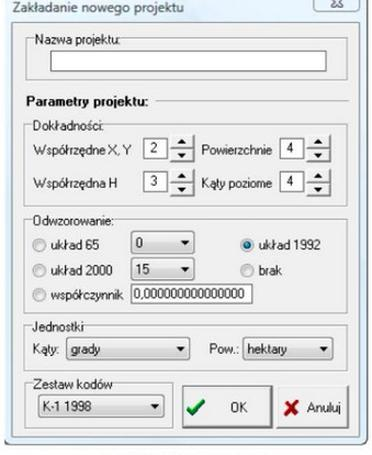
Południkiem osiowym w odwzorowaniu Gaussa-Krügera dla układu współrzędnych PL-2000 jest południk

A. 22°

B. 20°

C. 21°

D. 19°

Wybór jakiegokolwiek innego południka, takiego jak 22°, 20° czy 19°, nie jest zgodny z definicją osiowego południka w układzie PL-2000. Południki te mogą być mylone z innymi południkami, które nie są właściwymi osiowymi w kontekście określonego odwzorowania. Południk 22° z pewnością znajduje się na zachód od południka 21°, co prowadzi do zwiększenia zniekształceń w obszarze, który jest odwzorowywany. Z kolei południk 20° leży na wschód od 21°, co również nie jest odpowiednie w kontekście geodezyjnym. Wybór południka 19° jest jeszcze bardziej odległy od optymalnego, co w praktyce prowadzi do poważnych błędów w pomiarach i analizach przestrzennych. Typowym błędem myślowym jest założenie, że każdy południk w danej strefie będzie odpowiedni do użycia jako osiowy. W rzeczywistości, tylko konkretne południki są zaprojektowane do minimalizowania zniekształceń na danym obszarze. Dla geodetów, architektów i specjalistów zajmujących się planowaniem przestrzennym niezwykle istotne jest zrozumienie, jak odwzorowanie wpływa na dokładność danych geograficznych, a wybór niewłaściwego południka może prowadzić do błędnych decyzji projektowych i nieefektywnej pracy.

Pytanie 20

Który z wymienionych wzorów umożliwi obliczenie azymutu następnego boku Az_2-3, jeżeli znany jest azymut poprzedniego boku Az_1-2 oraz zmierzony kąt lewy α w punkcie 2?

A. Az2-3 = Az1-2 – α + 200g

B. Az2-3 = Az2-1 + α - 200g

C. Az2-3 = Az1-2 + α - 200g

D. Az2-3 = Az2-1 – α + 200g

Odpowiedź Az2-3 = Az1-2 + α - 200g jest prawidłowa, ponieważ przy obliczaniu azymutu kolejnego boku w geodezji stosujemy wzór, który uwzględnia azymut boku poprzedniego oraz pomierzony kąt lewy. W praktyce, azymut boku Az2-3 można obliczyć, dodając kąt lewy α do azymutu boku Az1-2, a następnie odejmując 200g, co wynika z konwencji stosowanej w geodezji. Zgodnie z zasadami, w przypadku pomiarów z użyciem teodolitu, kąt lewy jest mierzony w przeciwnym kierunku do ruchu wskazówek zegara, co wymaga uwzględnienia odpowiednich poprawek przy wyznaczaniu azymutu. Praktyczne zastosowanie tego wzoru widoczne jest w terenie, gdzie precyzyjne pomiary są kluczowe dla uzyskania dokładnych wyników w mapowaniu i inżynierii. Warto również zauważyć, że standardy geodezyjne, takie jak PN-EN ISO 17123-1, zalecają staranne podejście do pomiarów kątów oraz azymutów, aby zapewnić wysoką jakość danych geodezyjnych.

Pytanie 21

Azymut węzłowy został obliczony na podstawie 4 ciągów poligonowych, w których zarejestrowano:
− ciąg nr I - 5 kątów,
− ciąg nr II - 4 kąty,
− ciąg nr III - 3 kąty,
− ciąg nr IV - 2 kąty.
Który z ciągów ma największą wagę?

A. Ciąg II

B. Ciąg III

C. Ciąg IV

D. Ciąg I

Ciąg IV ma największą wagę, ponieważ zawiera najmniejszą liczbę pomierzonych kątów, co czyni go mniej obciążonym błędami pomiarowymi. W praktyce, im mniejsza ilość kątów w ciągu, tym większa jego waga, ponieważ zyskuje on na precyzji i wiarygodności w kontekście obliczeń azymutów. Ważenie ciągów kątowych opiera się na zasadzie, że każdy pomiar kątowy wprowadza potencjalny błąd, a im więcej pomiarów, tym suma błędów może być większa. Dlatego w geodezji i kartografii, stosując metody takie jak metoda najmniejszych kwadratów, preferuje się mniejsze ciągi pomiarowe dla uzyskania bardziej stabilnych i dokładnych wyników. Ponadto, w kontekście azymutów węzłowych, kluczowe jest także zrozumienie, że każdy pojedynczy kąt ma swoje znaczenie w rozrachunkach, a więc mniejsza ilość pomiarów w ciągu IV wpływa na jego większą wagę w całym procesie wyznaczania azymutów. Takie podejście jest zgodne z normami i dobrymi praktykami w dziedzinie geodezji.

Pytanie 22

Aby zmierzyć szczegóły sytuacyjne metodą ortogonalną, geodeta ustawił linię pomiarową AB, którą zmierzył ruletką pięć razy. Jeśli otrzymał następujące wyniki: 160,10 m; 160,12 m; 180,12 m; 160,11 m; 160,13 m, to długość boku AB jest obarczona błędem

A. grubym

B. przypadkowym

C. systematycznym

D. pozornym

Pomiar długości boku AB obarczony jest błędem grubym, ponieważ w dostarczonych wynikach pomiarów zauważalna jest jedna wartość znacznie odbiegająca od pozostałych. Wynik 180,12 m jest doskonale widocznym wyjątkiem, co sugeruje, że mógł być wynikiem pomyłki, na przykład błędnego odczytu, błędnego ustawienia ruletki, czy też nieprawidłowego pomiaru. W praktyce geodezyjnej, błędy grubym są najczęściej eliminowane przez powtarzanie pomiaru i porównywanie wyników, co może podnieść jakość danych. W takich przypadkach stosuje się również średnią arytmetyczną pozostałych pomiarów, aby uzyskać bardziej wiarygodny wynik. Ważne jest, by geodeci byli świadomi takich anomalii, ponieważ mogą one znacząco wpłynąć na późniejsze analizy geodezyjne i projektowe. Dobrą praktyką jest również stosowanie metod statystycznych do identyfikacji i eliminacji błędów grubych, co jest zgodne z normami ISO 17123 dotyczącymi pomiarów geodezyjnych.

Pytanie 23

Korzystając z danych zamieszczonych w tabeli, oblicz kąt skręcenia pomiędzy układami współrzędnych wtórnym i pierwotnym.

Numer punktu	Układ pierwotny		Układ wtórny
	X^p	Y^p	X^w	Y^w
1	100,00	100,00	400,00	400,00
2	123,00	134,00	377,00	366,00
3	145,00	162,00	355,00	338,00
4	200,00	200,00	300,00	300,00

A. 200g

B. 250g

C. 50g

D. 300g

Prawidłowa odpowiedź to 200g, co oznacza kąt skręcenia między układami współrzędnych wtórnym i pierwotnym. Aby obliczyć kąt skręcenia, ważne jest zrozumienie, jak układy współrzędnych są ze sobą powiązane. Kąt ten można określić poprzez analizę różnic między danymi w układzie pierwotnym a tymi w układzie wtórnym. W praktyce, poprawne obliczenie kąta skręcenia jest kluczowe w dziedzinach takich jak inżynieria, architektura oraz robotyka, gdzie precyzyjne określenie orientacji obiektów jest niezbędne do prawidłowego działania mechanizmów i systemów. Kiedy zmieniamy orientację układów współrzędnych, musimy uwzględnić nie tylko kąt, ale także zmiany w lokalizacji oraz ewentualne przekształcenia, które mogą wpłynąć na dalsze obliczenia. Znajomość prawidłowego obliczania kąta skręcenia jest zgodna z najlepszymi praktykami w zakresie projektowania systemów, w których precyzja ma kluczowe znaczenie dla ich funkcjonowania.

Pytanie 24

Jaką maksymalną liczbę boków może mieć jednostronnie nawiązany wielokąt?

A. 5 boków

B. 4 boki

C. 2 boki

D. 3 boki

Wybór innych opcji, takich jak 5, 3 czy 4 boki, wynika z nieporozumienia odnośnie definicji poligonów jednostronnie nawiązanych. Poligon ten, jak sama nazwa wskazuje, charakteryzuje się tym, że jest formą zamkniętą, której wierzchołki są połączone w sposób umożliwiający ich zamknięcie, jednakże jednocześnie nie może mieć więcej niż dwóch boków ze względu na reguły geometrii. W przypadku odpowiedzi wskazujących na 3 boki, 4 boki czy 5 boków, pojawia się typowy błąd myślowy związany z interpretacją poligonu jako figury wielokątnej, co wprowadza w błąd. Tego typu koncepcje są powszechnie spotykane, szczególnie w kontekście nauczania geometrii, gdzie uczniowie często mylą definicje figur. Aby wyjaśnić, dlaczego te odpowiedzi są nieprawidłowe, warto zaznaczyć, że każdy dodany bok w rzeczywistości przekształca jednostronnie nawiązany poligon w inną klasę figur, co narusza definicję jednostronnych poligonów. Z tego powodu, dla prawidłowego rozumienia koncepcji geometrycznych, kluczowe jest precyzyjne zaznajomienie się z definicjami i regułami rządzącymi poszczególnymi typami figur, co jest istotne w kontekście nauk matematycznych i inżynierskich.

Pytanie 25

W bazie danych dotyczącej obiektów topograficznych BDOT500 opisano sieć kanalizacyjną sanitarną oznaczeniami ksX300. Jakie jest źródło danych dotyczących lokalizacji tej sieci?

A. jest trudne do ustalenia

B. jest nieokreślone

C. pochodzi z materiałów archiwalnych

D. pochodzi z materiałów nieaktualnych

Wybór odpowiedzi sugerujących, że źródło danych pochodzi z materiałów archiwalnych, jest trudne do określenia lub jest nieaktualne, opiera się na błędnym rozumieniu charakterystyki i jakości danych w systemach geoinformacyjnych. Materiały archiwalne mogą zawierać wartościowe informacje, jednak ich wykorzystanie wiąże się z koniecznością krytycznej oceny ich aktualności oraz precyzyjności. W przypadku danych o sieci kanalizacyjnej, które są kluczowe dla planowania infrastruktury miejskiej, istotne jest, aby odnosić się do najnowszych i potwierdzonych zasobów. Uznanie, że źródło danych jest trudne do określenia, wskazuje na brak wiedzy na temat metod zbierania i weryfikacji danych, co jest istotnym elementem analizy przestrzennej. W kontekście praktycznym, takie podejście może prowadzić do poważnych błędów w projektowaniu i zarządzaniu sieciami, co jest niezgodne z normami branżowymi, które kładą nacisk na transparentność i weryfikowalność danych. Warto zwrócić uwagę, że w dużych projektach budowlanych, brak rzetelnych danych może prowadzić do nieprzewidzianych kosztów oraz opóźnień w realizacji, co podkreśla znaczenie dobrej praktyki w dokumentacji i aktualizacji danych geoinformacyjnych.

Pytanie 26

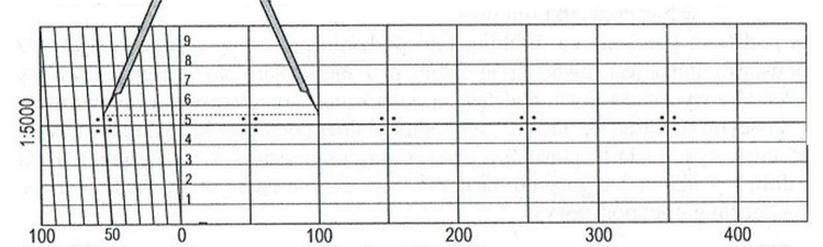
Wartość odczytu, którą wskazuje przestawiona podziałka transwersalna, wynosi

A. 155,0 m

B. 155,5 m

C. 55,0 m

D. 55,5 m

Odpowiedź 155,5 m jest poprawna, ponieważ aby prawidłowo odczytać wartość na przestawionej podziałce transwersalnej, należy zrealizować kilka kroków obliczeniowych. Pierwszym krokiem jest zidentyfikowanie wartości głównej podziałki, która w tym przypadku wynosi 250 m. Następnie dodajemy przesunięcie podziałki transwersalnej, które wynosi 5,5 m. W efekcie uzyskujemy 255,5 m. Zgodnie z zasadami odczytu wartości z podziałek, od tej liczby odejmujemy wartość początkową podziałki, która wynosi 100 m. W rezultacie 255,5 m - 100 m daje nam końcowy wynik 155,5 m. Umiejętność prawidłowego odczytu z podziałek jest niezbędna w wielu dziedzinach inżynierii, na przykład w geodezji, gdzie precyzyjne pomiary są kluczowe dla skutecznego planowania i realizacji projektów budowlanych. Standardy takie jak ISO 17123 definiują metody pomiarowe, co dodatkowo potwierdza istotność dokładnych odczytów w praktyce.

Pytanie 27

Fragment łączący dwa sąsiadujące punkty sytuacyjne tego samego obiektu określa się mianem

A. rzędną

B. podpórką

C. czołówką

D. odciętą

Wybór odciętej jako odpowiedzi jest nieporozumieniem związanym z terminologią geodezyjną. Odcięta odnosi się do poziomego lub pionowego skoku wartości w kontekście pomiarów, na przykład, w analizach funkcji w przestrzeni, ale nie jest terminem odnoszącym się do połączenia punktów sytuacyjnych obiektu. W praktyce, odcięta jest często używana w kontekście obliczeń różnicowych, gdzie analizuje się zmiany w wartościach pomiędzy różnymi punktami, jednak nie ma zastosowania w bezpośrednim łączeniu dwóch sąsiednich punktów. Podpórka z kolei odnosi się do wsparcia dla konstrukcji, a nie do geodezyjnego opisu relacji między punktami. W kontekście geodezji, podpórki mogą być używane w konstrukcjach, ale nie w sensie odnoszącym się do punktów sytuacyjnych. Rzędna, choć również związana z poziomem, odnosi się do wartości wysokości punktu w kontekście terenu, a nie do łączenia dwóch punktów. Zrozumienie tych terminów jest kluczowe, aby uniknąć typowych błędów myślowych, które mogą prowadzić do niepoprawnych wniosków w analizach przestrzennych. Kluczowe jest, aby zastosować właściwą terminologię w każdym kroku procesu pomiarowego, aby zapewnić klarowność i precyzję w dokumentacji oraz analizach geodezyjnych. Właściwe rozumienie czołówki i jej roli w łączeniu punktów sytuacyjnych jest fundamentem dla profesjonalnego podejścia w geodezji.

Pytanie 28

Do trwałych metod stabilizacji punktów osnowy poziomej nie zaliczają się

A. rurki stalowe

B. trzpienie metalowe

C. paliki drewniane

D. słupy betonowe

Paliki drewniane nie są odpowiednie do trwałego sposobu stabilizacji punktów osnowy poziomej z kilku powodów. Przede wszystkim, drewno jako materiał jest podatne na degradację, zwłaszcza w warunkach atmosferycznych, co prowadzi do utraty stabilności i dokładności pomiarów geodezyjnych. Z czasem paliki mogą gnić, ulegać deformacji lub przesuwać się w wyniku zmian wilgotności i temperatury. W praktyce geodezyjnej preferuje się materiały o wysokiej trwałości i odporności na czynniki zewnętrzne, takie jak metale i beton, które zapewniają długoterminową stabilność punktów osnowy. Na przykład, trzpienie metalowe i rurki stalowe, wykorzystywane w stabilizacji punktów, są odporne na korozję i mechaniczne uszkodzenia, co czyni je bardziej niezawodnymi w długim okresie. Zgodnie z normami geodezyjnymi, zastosowanie stałych punktów o wysokiej trwałości jest niezbędne do zapewnienia dokładności pomiarów i ich powtarzalności w czasie, co jest kluczowe w projektowaniu i realizacji inwestycji budowlanych oraz infrastrukturalnych.

Pytanie 29

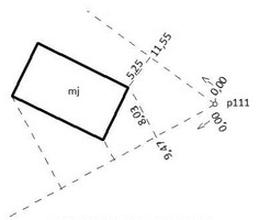
Jaką miarę kontrolną przy pomiarze szczegółów przedstawia rysunek?

A. Podpórkę.

B. Miarę przekątną.

C. Drugi niezależny pomiar.

D. Miarę czołową.

Poprawna odpowiedź to "drugi niezależny pomiar", ponieważ rysunek ilustruje metodę, która jest fundamentalna w analizie pomiarowej. Użycie drugiego niezależnego pomiaru to kluczowy sposób na zapewnienie precyzji i rzetelności wyników. W praktyce, polega to na wykonaniu ponownego pomiaru tego samego obiektu lub parametru przy użyciu tego samego narzędzia, co pozwala na porównanie wyników. Taka procedura jest zalecana w standardach metrologicznych, takich jak ISO 9001, gdzie podkreśla się znaczenie walidacji danych pomiarowych. W branży inżynieryjnej, na przykład podczas kalibracji przyrządów pomiarowych, drugi niezależny pomiar umożliwia wykrycie ewentualnych błędów systematycznych, co w rezultacie pozwala na ich korekcję. Dodatkowo, stosowanie tej metody w laboratoriach badawczych przyczynia się do zwiększenia pewności wyników oraz minimalizacji ryzyka błędów, co jest kluczowe w procesach podejmowania decyzji opartych na danych.

Pytanie 30

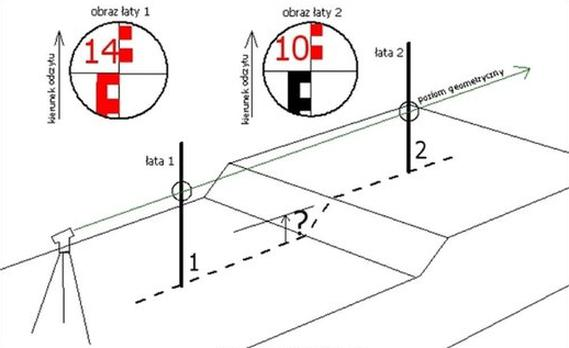
Ile wynosi różnica wysokości Δh pomiędzy punkami 1 i 2, na których ustawiono łaty niwelacyjne w sposób 1-2 przedstawiony na zamieszczonym rysunku?

A. 0,4 cm

B. 4,0 m

C. 4,0 cm

D. 0,4 m

Różnica wysokości Δh pomiędzy punktami 1 i 2 wynosi 0,4 m, co zostało uzyskane przez odjęcie wartości odczytanej na łacie niwelacyjnej w punkcie 2 (1,0 m) od wartości w punkcie 1 (1,4 m). Tego typu obliczenia są kluczowe w różnych dziedzinach inżynierii oraz budownictwa, umożliwiając określenie odpowiednich spadków terenu czy też przygotowanie projektów budowlanych, gdzie precyzyjne pomiary wysokości są niezbędne. W praktyce, często stosuje się łaty niwelacyjne w połączeniu z instrumentami takimi jak teodolity czy poziomice optyczne, co zwiększa dokładność pomiarów. Przykładowo, przy budowie dróg, niezbędne jest dokładne określenie różnic wysokości, aby zapewnić odpowiedni spadek odwadniający, co jest zgodne z normami branżowymi dotyczącymi budowy infrastruktury. Zrozumienie tego zagadnienia jest kluczowe dla profesjonalistów zajmujących się geodezją oraz projektowaniem przestrzennym.

Pytanie 31

Oś stanowiąca południki w odwzorowaniu Gaussa-Krugera w systemie współrzędnych PL-1992 to południk

A. 17o

B. 21o

C. 15o

D. 19o

Odpowiedź 19o jest jak najbardziej trafna. W systemie PL-1992, który jest jednym z ważniejszych układów używanych w Polsce, południk 19o to ten, który odpowiada strefie 5 w odwzorowaniu Gaussa-Krugera. To ważne, bo dzięki temu mamy jednolite dane geograficzne na mapach. W praktyce oznacza to, że w rejonie objętym tym południkiem, współrzędne są odwzorowywane w sposób, który minimalizuje zniekształcenia. To naprawdę istotne, szczególnie w inżynierii, planowaniu przestrzennym czy geodezji. Precyzyjne pomiary są kluczowe, bo od tego zależy rozwój infrastruktury i ochrona środowiska. Zrozumienie, jak działają układy współrzędnych, takie jak PL-1992, to podstawa, jeśli chcesz skutecznie korzystać z narzędzi GIS oraz robić analizy przestrzenne. To wszystko jest bardzo istotne w nowoczesnych badaniach geograficznych.

Pytanie 32

Na podstawie zamieszczonych w tabeli wyników pomiarów punktów kontrolowanych, oblicz przemieszczenie pionowe punktu nr 3.

Nr punktu	Pomiar pierwotny H_p [m]	Pomiar wtórny H_w [m]
1	521,2578	521,2480
2	521,2521	521,2410
3	521,2610	521,2554
4	521,2586	521,2533
5	521,2567	521,2458
6	521,2505	521,2412

A. -56 mm

B. +5,6 mm

C. -5,6 mm

D. +56 mm

Jeśli wybrałeś błędną odpowiedź, to może wynikać z niejasności, jak oblicza się przemieszczenie. Przemieszczenie pionowe punktu nr 3 nie może być dodatnie, bo to by znaczyło, że punkt się unosi, a my wiemy, że jest inaczej. Gdy mówimy o obniżeniu o -5,6 mm, to znaczy, że punkt jest niżej niż był. Często w analizach pomiarowych ludzie mylą znaki przy przemieszczeniach, co prowadzi do nieporozumień. Możliwe, że pomyliłeś przemieszczenie w górę z dodatnią wielkością, a to przez to mogą pojawić się błędne wnioski o stanie budowli. Niektórzy mogą też koncentrować się na wartościach bezwzględnych, nie zauważając kierunku przemieszczenia, co w inżynierii jest kluczowe. Zawsze warto mieć na oku zasady, które mówią, że ujemne wartości to obniżenie. W bardziej skomplikowanych analizach ważne jest używanie odpowiednich metod i narzędzi, żeby zrozumieć ruchy gruntów i ich wpływ na budowle.

Pytanie 33

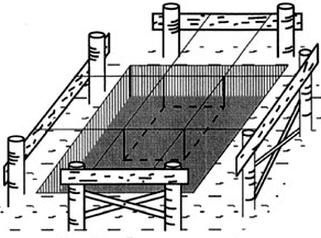
Jak nazywają się konstrukcje drewniane przedstawione na rysunku, służące do utrwalenia wytyczonych osi konstrukcyjnych obiektu budowlanego?

A. Trójkąty skarpowe.

B. Krzyże niwelacyjne.

C. Stopy fundamentowe.

D. Ławy ciesielskie.

Ławy ciesielskie to naprawdę ważne konstrukcje w budownictwie. Służą jako stabilne wsparcie, które pomaga w wyznaczaniu osi konstrukcyjnych, co jest kluczowe, żeby wszystko było zrobione porządnie. Dzięki nim łatwiej jest ustalić poziom fundamentów, co z kolei ma duże znaczenie dla dalszej budowy. Na przykład, gdy robisz podłoże pod schody czy strop, obecność ław ciesielskich pomaga zachować właściwe kąty i linie. Fajnie jest też wiedzieć, że stosowanie ich zgodnie z zasadami branżowymi to dobra praktyka, bo dzięki temu unikamy błędów, które mogą generować dodatkowe koszty. Z mojego doświadczenia, warto też sprawdzić stabilność tych ław przed rozpoczęciem kolejnych etapów budowy, żeby mieć pewność, że wszystko idzie jak należy.

Pytanie 34

Na rysunku przedstawiono wyświetlacz niwelatora

A. kodowego.

B. optycznego.

C. rotacyjnego.

D. laserowego.

Wyświetlacz zaprezentowany na rysunku należy do niwelatora kodowego, który jest zaawansowanym narzędziem pomiarowym używanym w geodezji do precyzyjnego ustalania różnic wysokości. Niwelatory kodowe wykorzystują specjalnie zaprojektowane łaty, na których umieszcza się kod kreskowy. Odczyty wysokości są następnie automatycznie rejestrowane przez urządzenie, co znacznie zwiększa dokładność oraz efektywność pomiarów. Dzięki zastosowaniu technologii cyfrowej, niwelatory kodowe eliminują błędy związane z manualnym odczytem, co jest szczególnie istotne podczas realizacji dużych projektów budowlanych czy infrastrukturalnych. W praktyce, niwelatory kodowe są wykorzystywane do precyzyjnego pomiaru terenu, a także w pracach związanych z projektowaniem i nadzorowaniem robót budowlanych. Stosowanie niwelatorów kodowych jest zgodne z aktualnymi standardami branżowymi, co zapewnia wysoką jakość oraz wiarygodność wyników pomiarów.

Pytanie 35

Który z poniższych obiektów wymaga obowiązkowego wytyczenia geodezyjnego oraz inwentaryzacji powykonawczej?

A. Przyłącze wodociągowe

B. Sygnał drogowy.

C. Plac zabaw.

D. Ogrodzenie stałe.

Przyłącze wodociągowe podlega obowiązkowemu wytyczeniu geodezyjnemu oraz inwentaryzacji powykonawczej, ponieważ jest to element infrastruktury technicznej, który ma istotne znaczenie dla organizacji przestrzennej oraz funkcjonowania sieci wodociągowej. Wytyczenie geodezyjne pozwala na precyzyjne określenie jego lokalizacji w terenie, co jest kluczowe dla uniknięcia kolizji z innymi instalacjami, co może prowadzić do kosztownych napraw i zakłóceń w dostawie wody. Inwentaryzacja powykonawcza ma na celu dokumentację stanu przyłącza po zakończeniu prac budowlanych, co jest istotne z punktu widzenia zarządzania infrastrukturą oraz jej późniejszej eksploatacji. Przykładem może być sytuacja, w której inwestor budowlany zleca wykonanie przyłącza wodociągowego, a następnie po zakończeniu prac geodeta przeprowadza inwentaryzację, aby potwierdzić zgodność wykonanego przyłącza z projektem. Zgodnie z obowiązującymi w Polsce przepisami prawa budowlanego oraz standardami geodezyjnymi, takie działania są niezbędne w celu zapewnienia bezpieczeństwa użytkowania oraz ochrony interesów publicznych.

Pytanie 36

Jakich informacji nie powinno się zamieszczać w opisie obiektu podczas aktualizacji mapy zasadniczej?

A. Numeru porządkowego obiektu

B. Oznaczenia literowego źródła danych o lokalizacji

C. Oznaczenia literowego funkcji obiektu

D. Liczby kondygnacji nadziemnych

Oznaczenie literowe źródła danych o położeniu to informacja, która nie jest istotna dla opisu budynku w kontekście aktualizacji mapy zasadniczej. W praktyce, aktualizacja ta powinna skupiać się na danych, które są kluczowe dla identyfikacji i charakterystyki obiektów budowlanych. Numer porządkowy budynku oraz oznaczenie literowe funkcji budynku są istotne dla klasyfikacji i lokalizacji obiektów, co jest zgodne z obowiązującymi normami w zakresie ewidencji budynków. Liczba kondygnacji nadziemnych również ma znaczenie, ponieważ wpływa na klasyfikację obiektów oraz ich przeznaczenie. Oznaczenie źródła danych jest natomiast informacją techniczną, która dotyczy pochodzenia danych, a nie samego budynku. W dobrych praktykach kartograficznych i urbanistycznych koncentrujemy się na danych, które mają bezpośredni wpływ na planowanie przestrzenne oraz podejmowanie decyzji inwestycyjnych.

Pytanie 37

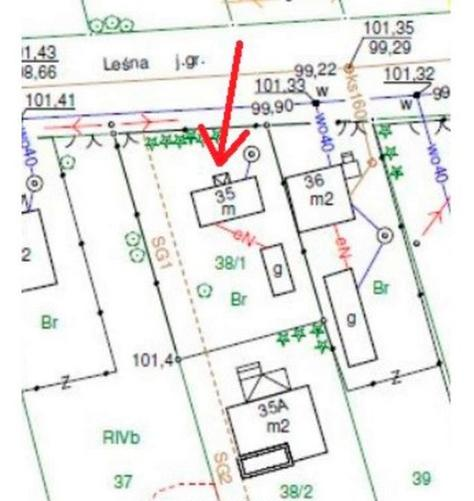
Na przedstawionej mapie zasadniczej strzałką wskazano

A. rampę.

B. ganek.

C. taras.

D. nawis.

Ganek to architektoniczny element budynku, zazwyczaj zadaszony i otwarty, który znajduje się przy głównym wejściu. Na przedstawionej mapie zasadniczej obiekt oznaczony strzałką odpowiada temu opisowi, co czyni odpowiedź poprawną. Ganki są powszechnie stosowane w projektach budowlanych jako sposób na ochronę wejścia przed warunkami atmosferycznymi, a także jako estetyczny element poprawiający wizualny odbiór budynku. W profesjonalnym projektowaniu architektonicznym ganek może być zaprojektowany na wiele sposobów, w zależności od stylu budynku oraz lokalnych uwarunkowań klimatycznych. Warto również zaznaczyć, że w projektach budowlanych często uwzględnia się takie elementy w ramach norm budowlanych, co podkreśla ich znaczenie zarówno funkcjonalne, jak i estetyczne. Znajomość terminologii związanej z architekturą, w tym różnicy między gankiem a innymi elementami, takimi jak taras czy nawis, jest kluczowa dla każdego architekta.

Pytanie 38

Jakie jest wartość błędu względnego pomiaru długości odcinka wynoszącego 120 m, przy średnim błędzie pomiaru równym ±2 cm?

A. 1:6000

B. 1:8000

C. 1:2000

D. 1:4000

Błąd względny pomiaru to stosunek błędu pomiaru do wartości rzeczywistej, co można wyrazić wzorem: błąd względny = (błąd pomiaru / wartość rzeczywista). W przypadku podanego odcinka o długości 120 m i błędzie pomiaru wynoszącym ±2 cm, najpierw musimy zamienić długość odcinka na centymetry, co daje 12000 cm. Następnie obliczamy błąd względny: ±2 cm / 12000 cm = 0,0001667. Przekształcając ten wynik na postać ułamka dziesiętnego, otrzymujemy 1:6000. Takie obliczenia są kluczowe w pomiarach inżynieryjnych, gdzie precyzja jest niezwykle ważna. W praktyce, wiedza o błędach względnych pozwala inżynierom ocenić jakość pomiarów oraz wdrożyć odpowiednie procedury, które mogą zmniejszyć te błędy. Warto też zaznaczyć, że błąd względny powinien zawsze być analizowany w kontekście standardów pomiarowych i jakości, takich jak ISO 9001, które podkreślają znaczenie dokładności i powtarzalności pomiarów.

Pytanie 39

Zbiór punktów o współrzędnych X, Y ustalonych w sieciach geodezyjnych o najwyższej precyzji określamy mianem osnowy

A. niwelacyjną

B. podstawową

C. pomiarową

D. dokładną

Zrozumienie pojęcia osnowy geodezyjnej jest kluczowe dla prawidłowego podejścia do zagadnień pomiarowych. Wybór nieadekwatnych terminów, takich jak osnowa szczegółowa, niwelacyjna, czy pomiarowa, może prowadzić do istotnych nieporozumień. Osnowa szczegółowa odnosi się do lokalnych układów współrzędnych, które są wykorzystywane w bardziej precyzyjnych pomiarach, ale nie mają tego samego znaczenia co osnowa podstawowa. Osnowa niwelacyjna dotyczy pomiarów wysokości, bazując na poziomach referencyjnych, co jest zaledwie jednym z aspektów geodezji, a nie całościowym podejściem do układu współrzędnych. W kontekście osnowy pomiarowej, jest to termin ogólny, który nie odnosi się do specyficznych, precyzyjnych punktów, jak ma to miejsce w przypadku osnowy podstawowej. Typowe błędy myślowe polegają na myleniu tych pojęć i przypisywaniu im rangi, której nie powinny mieć, co może skutkować poważnymi konsekwencjami w zakresie jakości i dokładności pomiarów. W praktyce, niezrozumienie różnic pomiędzy tymi rodzajami osnowy może prowadzić do błędów w projektowaniu i wykonaniu prac geodezyjnych, co z kolei wpływa na dalsze procesy inżynieryjne oraz planistyczne.

Pytanie 40

Ile wynosi błąd średni $ m_P $ położenia punktu osnowy realizacyjnej, jeżeli błędy współrzędnych X i Y tego punktu wynoszą odpowiednio: $ m_x = 0,4 $ cm, $ m_y = 0,3 $ cm oraz $ m_P = \pm \sqrt{m_x^2 + m_y^2} $.

A. $ m_P = \pm 0,4 $ cm

B. $ m_P = \pm 0,9 $ cm

C. $ m_P = \pm 0,6 $ cm

D. $ m_P = \pm 0,5 $ cm

W tej sytuacji prawidłowo określono błąd średni położenia punktu osnowy realizacyjnej, wykorzystując wzór $ m_P = \pm \sqrt{m_x^2 + m_y^2} $. To dokładnie tak, jak się robi w geodezji – kiedy mamy błędy współrzędnych ortogonalnych (czyli X i Y), musimy policzyć ich „łączny” wpływ na położenie punktu. Ten wzór jest w zasadzie standardem branżowym i pochodzi bezpośrednio z teorii błędów, a dokładniej z obliczania błędu średniego prostokątnego. W praktyce, dla błędów $ m_x = 0,4 $ cm i $ m_y = 0,3 $ cm liczymy: $ m_P = \sqrt{0,4^2 + 0,3^2} = \sqrt{0,16 + 0,09} = \sqrt{0,25} = 0,5 $ cm – i właśnie to, moim zdaniem, świadczy o bardzo dobrej znajomości podstaw pomiarów sytuacyjnych. Taka metoda jest uniwersalna, bo niezależnie od tego, ile wynoszą składowe, zawsze suma błędów wypadkowych daje nam rzeczywiste przybliżenie niepewności położenia punktu w terenie. W codziennej pracy geodety, podobne obliczenia są konieczne choćby przy zakładaniu osnów realizacyjnych pod obiekty budowlane czy analizie dokładności robót tyczenia. No i szczerze mówiąc, nie wyobrażam sobie, żeby ktoś profesjonalnie podchodził do tematów związanych z precyzyjnym położeniem punktów bez stosowania tego dokładnie wzoru – to podstawa, także w kontrolach geodezyjnych czy późniejszych pomiarach powykonawczych. Dobrze też pamiętać, że właśnie takie podejście pozwala spełnić wymogi rozporządzeń dotyczących dokładności osnowy realizacyjnej, gdzie opisane są minimalne wymagania dla błędów położenia. No i, co ważne, to nie tylko teoria – od tego zależy późniejsza jakość i bezpieczeństwo budowanych obiektów!"

Rozpocznij nowy egzamin

Powrót do strony głównej