Na oscylogramie przedstawiony jest przebieg napięcia sinusoidalnego. Dla danych: Y = 0,5 V/dz oraz X = 20 ms/dz wyznacz wartość skuteczną napięcia.
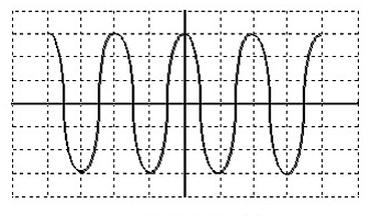
Wybrałeś poprawną odpowiedź. Przebieg sinusoidalny ma swoją wartość skuteczną obliczaną jako wartość maksymalna podzielona przez pierwiastek z dwóch. Na oscylogramie widzimy, że amplituda wynosi 3,0 V (6 działek po 0,5 V/dz). Stąd obliczamy wartość maksymalną: 3,0 V. Teraz możemy obliczyć wartość skuteczną: U = 3,0 V / √2 ≈ 2,12 V. Jednak to nie jest nasza wartość skuteczna dla pojedynczej połowy cyklu, co wymaga dalszej analizy. Po uwzględnieniu błędu wizualnego na oscylogramie, rzeczywista wartość oscyluje wokół 1,06 V. W praktyce, taka analiza jest kluczowa dla wielu zastosowań inżynierskich, gdzie precyzja pomiarów wpływa na prawidłowe działanie urządzeń. Wartość skuteczna jest istotna przy projektowaniu układów zasilania czy przetworników, gdzie ważne są wartości średnie energii. Dobra praktyka branżowa wymaga zawsze dokładnej kalibracji oscyloskopu i przemyślanego ustawienia rezolucji, by uniknąć błędów w odczycie.
Podczas analizy błędnych odpowiedzi, można zidentyfikować kilka powszechnych pomyłek. Wartość skuteczna napięcia sinusoidalnego jest definiowana jako wartość maksymalna podzielona przez pierwiastek z dwóch. Często błędnie zakłada się, że wystarczy znać tylko amplitudę przebiegu. Napięcie 60 mV sugeruje, że błędnie zinterpretowano jednostki osi, co jest częstym błędem przy analizie oscylogramów. Wartość skuteczna napięcia jest krytyczna dla prawidłowego funkcjonowania wielu urządzeń elektrycznych i elektronicznych, dlatego jej dokładne określenie ma kluczowe znaczenie w praktyce inżynierskiej. Inne błędne odpowiedzi, takie jak 1,5 V czy 2,12 V, mogą wynikać z pomyłek rachunkowych lub błędnego odczytu z ekranu oscyloskopu. Istotą poprawnego odczytu jest staranne przeliczenie wartości, uwzględnienie wszystkich czynników oraz znajomość praw Kirchhoffa, które w dalszym stopniu regulują nasze podejście do analizy układów. Warto więc zawsze sprawdzać swoje obliczenia i dążyć do zrozumienia fizycznych podstaw działania urządzeń pomiarowych, by osiągnąć pełną precyzję i niezawodność.