W celu określenia wartości rezystancji Rf jednej fazy uzwojenia stojana silnika elektrycznego skojarzonego w trójkąt należy zmierzyć rezystancje RUV, RVW, RWU i obliczyć ją z zależności
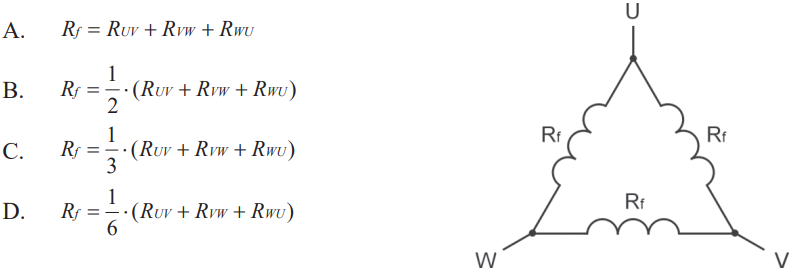
Wybór odpowiedzi B jest trafny, ponieważ opisuje prawidłową metodę obliczania wartości rezystancji jednej fazy uzwojenia stojana w układzie połączeń trójkąta. W układzie trójkąta, kiedy mierzymy rezystancje między wyprowadzeniami, takie jak RUV, RVW i RWU, każda z nich obejmuje dwie z trzech rezystancji fazowych. Aby znaleźć wartość jednej z nich, stosujemy równanie Rf = 1/2 * (RUV + RVW + RWU). Ten wzór wynika z faktu, że każda zmierzona rezystancja jest sumą rezystancji dwóch faz. Praktyczne zastosowanie tego wzoru można znaleźć w diagnostyce i konserwacji silników elektrycznych, gdzie ważne jest, aby zapewnić równomierne obciążenie i uniknąć przegrzewania. Wiedza ta jest fundamentem dla techników zajmujących się naprawą i utrzymaniem silników w dobrym stanie, zgodnie z najlepszymi praktykami w branży. Z mojego doświadczenia, prawidłowe zrozumienie tych zasad pozwala na szybkie i skuteczne identyfikowanie problemów w systemach zasilania.
Niepoprawne podejścia wynikają z błędnego zrozumienia, jak działają połączenia w układzie trójkąta oraz jakie są ich właściwości elektryczne. Odpowiedzi A, C i D zakładają błędne współczynniki w obliczeniach dla rezystancji fazowej. W przypadku A, założenie, że Rf = RUV + RVW + RWU, jest niepoprawne, ponieważ ignoruje się fakt, że każda z tych zmierzonych rezystancji obejmuje dwie rezystancje fazowe. W odpowiedziach C i D, współczynniki 1/3 i 1/6 są używane bez uzasadnienia; takie podejście nie ma oparcia w teorii obwodów dla układów połączeń trójkąta. Często takie błędy wynikają z braku zrozumienia równoległego i szeregowego charakteru połączeń oraz ich wpływu na mierzone wartości. Typowym błędem jest też nieodróżnianie połączeń gwiazdowych i trójkątowych, co prowadzi do niewłaściwego zastosowania wzorów. Zrozumienie tego, jak właściwie interpretować pomiary rezystancji, jest kluczowe w pracy z układami elektrycznymi i pozwala na prawidłowe diagnozowanie i rozwiązywanie problemów.