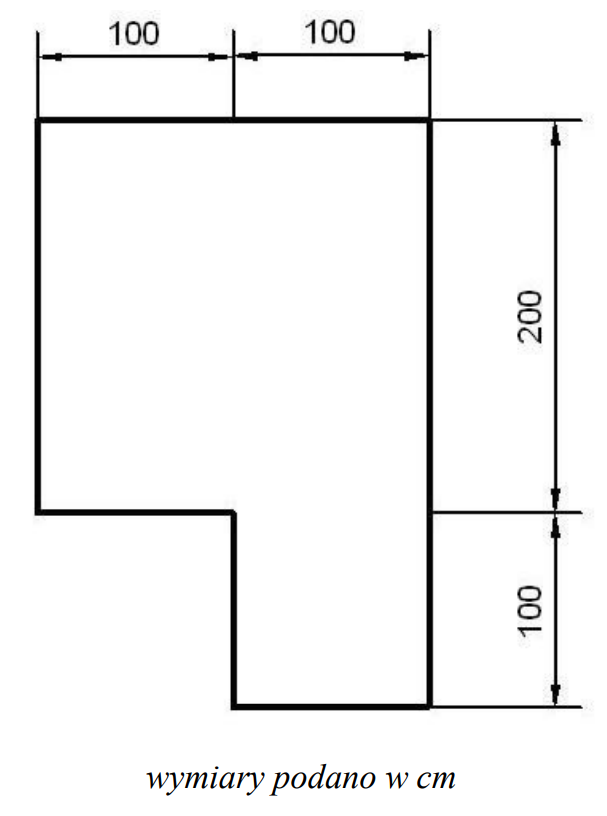
Dokładne obliczenie powierzchni posadzki na podstawie rysunku wymaga podzielenia figury na prostsze kształty, które łatwiej policzyć. W tym przypadku mamy jeden duży prostokąt o wymiarach 200 cm x 200 cm, z którego trzeba odjąć mniejszy prostokąt o wymiarach 100 cm x 100 cm, bo ta część jakby jest „wycięta”. Cały duży prostokąt to 4 m² (bo 2 m x 2 m), ale wtedy byśmy zapomnieli o tej wnęce po prawej stronie. Najprościej podzielić całość na dwa prostokąty: pierwszy 200 cm x 200 cm (czyli 4 m²), a drugi 100 cm x 100 cm (1 m²) – ta wnęka dodaje się do powierzchni głównej. Czyli 4 m² + 1 m² = 5 m². To dość typowe zadanie na obmiar, które bardzo często pojawia się nie tylko na egzaminach, ale też w codziennej pracy, kiedy trzeba zamówić materiał lub rozliczyć się z inwestorem. Moim zdaniem regularne ćwiczenie takiego typu zadań naprawdę się przydaje, bo na budowie liczy się precyzja i znajomość prostych metod podziału powierzchni. Zgodnie z dobrą praktyką branżową, zawsze warto sprawdzić dwa razy wyliczenia i upewnić się, że nie pomijamy żadnych wnęk ani wypustek. Takie podejście doceniają inspektorzy i inwestorzy. Jeśli masz jeszcze wątpliwości, polecam ćwiczyć podobne rysunki samodzielnie, żeby dojść do wprawy.
Przy obliczaniu powierzchni posadzki łatwo wpaść w pułapkę, jeśli bazujemy tylko na ogólnym wrażeniu kształtu albo nie rozbijamy figury na prostsze elementy. W tym konkretnym przypadku intuicyjne założenie, że kształt jest zbliżony do kwadratu 3 m x 2 m i stąd pojawi się wynik 6 m², nie uwzględnia wnęki, której nie powinno się doliczać podwójnie lub odejmować w nieprawidłowy sposób. Wynik 8 m² lub 9 m² to z kolei efekt błędnego zsumowania wszystkich boków jako niezależnych prostokątów lub nieuwzględnienia, że część powierzchni jest wycięta, a nie doliczana. Takie nieścisłości pojawiają się często, gdy nie rysuje się pomocniczych linii i nie dzieli całej powierzchni na prostokąty, które łatwo policzyć oddzielnie, a potem złożyć wynik w całość. Moim zdaniem, kluczowym błędem jest nieuwzględnienie „wcięcia” – tej wnęki o wymiarach 100 x 100 cm. Z praktyki wiem, że często uczniowie zapominają, że pole powierzchni to suma pól prostokątów, a nie suma długości boków. W branży, zgodnie ze standardami obmiarowymi, każde pomieszczenie należy analizować pod kątem nietypowych kształtów i doliczać lub odejmować te fragmenty, które faktycznie mają być objęte pracami. Najlepiej zawsze rozrysować sobie pomocniczą siatkę na rysunku i krok po kroku policzyć poszczególne prostokąty, żeby uniknąć takich błędów. Warto też wiedzieć, że w przypadku zabezpieczeń chemoodpornych zbyt zawyżony lub zaniżony metraż może prowadzić do strat finansowych lub problemów przy odbiorze robót. Opieranie się tylko na szacunkach lub zaokrąglaniu na oko to typowy błąd początkujących – lepiej poświęcić chwilę dłużej na dokładne liczenie.