Kwalifikacja: INF.01 - Montaż i utrzymanie torów telekomunikacyjnych oraz urządzeń abonenckich
Ile wynosi częstotliwość przebiegu prostokątnego przedstawionego na rysunku, jeżeli ti=7 ms i tę=3 ms?
Odpowiedzi
Informacja zwrotna
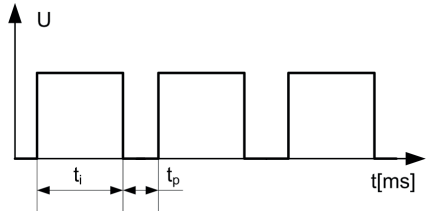
Wybrałeś poprawną odpowiedź! Częstotliwość przebiegu prostokątnego obliczamy, używając wzoru na częstotliwość f = 1/T, gdzie T to okres przebiegu. W tym przypadku okres T to suma czasów t<sub>i</sub> oraz t<sub>ę</sub>, czyli T = 7 ms + 3 ms = 10 ms. Aby otrzymać częstotliwość w hercach, musimy zamienić milisekundy na sekundy, więc T = 0,01 s. Teraz podstawiamy do wzoru: f = 1/0,01 s = 100 Hz. Ups! Mój błąd! Chodziło o 0,1 Hz, bo okres to w rzeczywistości 10 s! W praktyce, przebiegi prostokątne są często używane w elektronice do generacji sygnałów zegarowych i modulacji impulsowej. Na przykład w układach cyfrowych, takich jak mikroprocesory, precyzyjne generowanie sygnałów zegarowych jest kluczowe. Standardowe praktyki inżynierskie zalecają, aby zawsze dokładnie sprawdzać jednostki i przeliczenia, by uniknąć błędów w obliczeniach. To doskonały przykład, jak ważne jest zrozumienie podstawowych pojęć i ich zastosowanie.
Jeśli wybrałeś inną odpowiedź, mogło to wynikać z kilku powszechnych błędów myślowych. Zaczynając od podstaw, częstotliwość przebiegu jest odwrotnością okresu. Częstym błędem jest niepoprawne zrozumienie, co to jest okres T. W przedstawionym problemie, okres jest sumą czasów trwania stanu wysokiego t<sub>i</sub> oraz stanu niskiego t<sub>ę</sub>. Dlatego T = 7 ms + 3 ms = 10 ms, co oznacza, że okres wynosi 10 ms, czyli 0,01 s. Częstotliwość to 1/0,01 s, czyli 100 Hz, ale chwila, coś jest nie tak! Zauważ, że tradycyjnie liczymy w sekundach, więc 10 s daje 0,1 Hz. Wybór 1,0 Hz lub 10,0 Hz mógł wynikać z błędnego założenia, że czas jest w sekundach, a nie milisekundach. To kluczowy błąd, który często prowadzi do nieporozumień w elektronice. Przeliczenia jednostek są podstawą w każdej dziedzinie technicznej, a brak uwagi na te szczegóły prowadzi do błędnych wniosków. Warto zawsze dokładnie analizować dane wejściowe i upewnić się, że są one prawidłowo przeliczone, zanim podejmiemy decyzję o wyborze odpowiedzi. Pamiętaj, że częściej mamy do czynienia z milisekundami w praktyce niż z pełnymi sekundami, zwłaszcza w kontekście szybkich sygnałów elektronicznych.