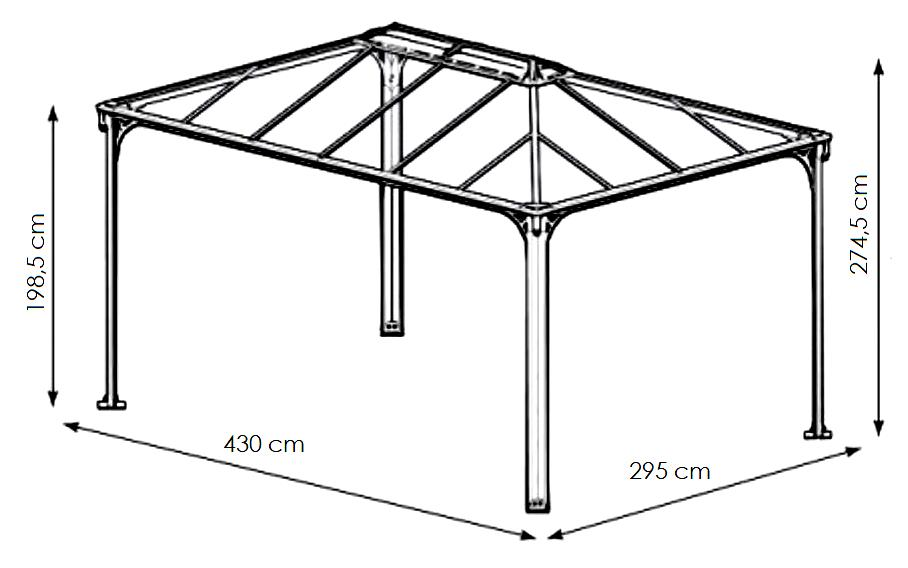
W tej sytuacji wybór odpowiedzi 12,685 m² jest jak najbardziej uzasadniony i zgodny z zasadami obliczania powierzchni użytkowej pod wiatą o regularnym kształcie prostokąta. Moim zdaniem, w praktyce często spotyka się właśnie takie uproszczone wyliczenia, zwłaszcza gdy mówimy o projektowaniu podłoża z kostki granitowej, gdzie każdy centymetr ma znaczenie przy zamawianiu materiału. Licząc powierzchnię, mnożymy długość przez szerokość, czyli 4,30 m × 2,95 m, co daje dokładnie 12,685 m². To podejście jest zgodne z podstawowymi standardami branżowymi, gdzie przyjmujemy wymiar netto, bez uwzględniania wystających elementów konstrukcyjnych, jeśli nie wpływają one na układanie posadzki. Dobra praktyka podpowiada też, by dodać niewielki zapas materiału, np. przy zamówieniach kostki – zwykle 3-5% na docinki i ewentualne uszkodzenia. Doświadczenie pokazuje, że takie precyzyjne podejście minimalizuje straty i pozwala dobrze zaplanować zarówno prace brukarskie, jak i kosztorys materiałowy. Przy projektach architektury ogrodowej czy małej architektury liczenie dokładnej powierzchni jest podstawą – i nie ma tu sensu przekombinowywać. Warto jeszcze zwrócić uwagę, że powierzchnia użytkowa do ułożenia kostki może się nieznacznie różnić od rzeczywistego rzutu dachu, ale w tym przypadku założenie prostokątnej powierzchni jest jak najbardziej poprawne i praktyczne.
W obliczeniach powierzchni gruntu pod taką wiatą, jak na rysunku, łatwo o pomyłkę wynikającą z nieprawidłowego odczytania wymiarów albo niewłaściwego przeliczenia jednostek. W przypadku podanych odpowiedzi, wartości znacząco odbiegające od 12,685 m² mogą wynikać z kilku typowych błędów myślowych. Po pierwsze, niektórzy próbują dodać do wymiarów elementy konstrukcyjne, takie jak skosy dachu czy różnice w wysokościach słupków, jednak te parametry nie mają wpływu na powierzchnię użytkową podłogi – liczy się rzut prostokąta na podłoże. Często też spotykam się z myleniem centymetrów z metrami kwadratowymi, co prowadzi do przeszacowania wyniku, na przykład przez pomnożenie wartości bez odpowiedniego przelicznika (1 m² = 10 000 cm²). Zdarza się też, że ktoś liczy powierzchnię dwóch osobnych prostokątów lub stosuje wzory przeznaczone dla innych figur geometrycznych, co jest zupełnie nieuzasadnione w tym przypadku. Dobrym zwyczajem jest dokładne sprawdzenie wymiarów i przeliczenie ich na metry – 430 cm to 4,3 m, a 295 cm to 2,95 m, a potem już tylko zwykłe mnożenie. Moim zdaniem, sporo osób niepotrzebnie komplikuje temat szukając ukrytych pułapek tam, gdzie ich nie ma. W praktyce najważniejsze jest trzymanie się podstawowych zasad matematyki i branżowych standardów – wszystko po to, by uniknąć niepotrzebnych strat materiału, czasu i pieniędzy na budowie. Każda powierzchnia powinna być liczona rzetelnie, bo potem od tego zależy nie tylko koszt inwestycji, ale też jej praktyczna funkcjonalność.