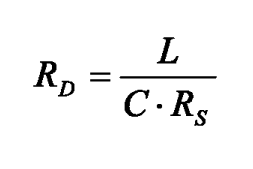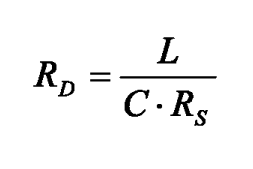Ten wzór pozwala wyznaczyć rezystancję dynamiczną obwodu rezonansowego, co jest jednym z kluczowych parametrów przy projektowaniu filtrów i układów rezonansowych. W praktyce, rezystancja dynamiczna (RD) informuje nas, jak bardzo obwód jest 'odporny' na straty energii przy pracy na częstotliwości rezonansowej. Im wyższa jest ta rezystancja, tym ostrzejsza i skuteczniejsza jest selektywność filtra – czyli lepiej tłumi sygnały poza pasmem. Z mojego doświadczenia, w branży elektronicznej często bagatelizuje się ten parametr na korzyść dobroci, a moim zdaniem to błąd, bo dokładna analiza RD pozwala przewidzieć, ile realnie energii będziemy tracić, np. w precyzyjnych układach radiowych czy pomiarowych. Wzór opiera się na wartościach indukcyjności (L), pojemności (C) i szeregowej rezystancji strat (RS) i jest szeroko stosowany w obliczeniach dla obwodów równoległych LC. Warto pamiętać, że normy np. IEC czy ogólnie przyjęte wytyczne projektowania filtrów zalecają analizę rezystancji dynamicznej jako element doboru komponentów o możliwie małych stratach. Często stosuję ten wzór przy doborze cewek i kondensatorów w aplikacjach audio i RF, bo pozwala mi to przewidzieć, jak zmieni się charakterystyka filtra przy zastosowaniu różnych podzespołów. Zdecydowanie warto znać i rozumieć ten parametr, bo ma realny wpływ na stabilność i sprawność całego układu.
Wzór zaprezentowany na ilustracji to klasyczna zależność pozwalająca wyznaczyć rezystancję dynamiczną obwodu rezonansowego LC, uwzględniającą zarówno indukcyjność, pojemność, jak i straty szeregowe. Często można się spotkać z przeświadczeniem, że skoro w wzorze występują L i C, to dotyczy on częstotliwości rezonansowej lub dobroci obwodu. To błąd – częstotliwość rezonansowa wylicza się ze wzoru f₀ = 1/(2π√(LC)), gdzie nie ma miejsca na rezystancję szeregową, a jej wartość zależy wyłącznie od parametrów biernych. Innym typowym nieporozumieniem jest utożsamianie tej zależności z obliczaniem indukcyjności uzwojenia, natomiast w praktyce L w tym równaniu jest wartością wejściową, a nie niewiadomą. Spotyka się też mylenie rezystancji dynamicznej z dobrocią (Q), bo oba pojęcia są związane z selektywnością układu, ale dobroć wylicza się jako stosunek energii zgromadzonej do strat energii na cykl, nie zaś bezpośrednio według tego wzoru. Często w praktyce technicznej spotykam się z tym, że początkujący projektanci przyjmują uproszczone założenia, ignorując wpływ rezystancji dynamicznej na kształtowanie szerokości pasma czy tłumienie obwodu. W branży elektronicznej od lat zaleca się uwzględnianie zarówno dobroci, jak i rezystancji dynamicznej, by precyzyjnie przewidzieć charakterystykę filtra, zwłaszcza w układach RF i audio, gdzie straty mają realny wpływ na jakość sygnału. Z mojego punktu widzenia, zrozumienie różnic pomiędzy tymi parametrami jest podstawą dobrej praktyki projektowej.