Ile wynosi całkowita moc prądu stałego wydzielona na rezystorach w układzie przedstawionym na schemacie, jeżeli R1 = 14 Ω, a R2 = R3 = 28 Ω
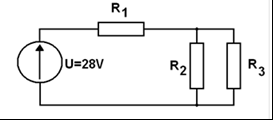
W tym zadaniu kluczowe jest poprawne rozpoznanie połączeń rezystorów i zastosowanie podstawowych praw obwodów prądu stałego. Na schemacie widzimy źródło napięcia 28 V, szeregowo włączony rezystor R1 = 14 Ω oraz gałąź równoległą złożoną z R2 i R3, gdzie R2 = R3 = 28 Ω. Najpierw upraszczamy część równoległą: dwie jednakowe rezystancje w połączeniu równoległym zastępujemy rezystancją zastępczą R23 = (R2·R3)/(R2+R3). Dla dwóch równych oporów jest to po prostu połowa wartości jednego z nich, czyli R23 = 28 Ω / 2 = 14 Ω. Teraz cały obwód sprowadza się do dwóch rezystorów połączonych szeregowo: R1 = 14 Ω i R23 = 14 Ω, więc rezystancja całkowita wynosi Rz = 14 Ω + 14 Ω = 28 Ω. Korzystamy z prawa Ohma: I = U / Rz = 28 V / 28 Ω = 1 A. Mając prąd w obwodzie, możemy policzyć całkowitą moc wydzielaną na rezystorach: P = U·I = 28 V · 1 A = 28 W. Można to też policzyć ze wzoru P = U² / Rz = 28² / 28 = 28 W, co ładnie się zgadza. W praktyce lotniczej taki sposób liczenia mocy jest bardzo ważny, bo instalacje 28 V DC są standardem w wielu statkach powietrznych i trzeba umieć szybko oszacować, jaką moc wydzielą rezystory, przewody czy odbiorniki, żeby nie przegrzać elementów, dobrać właściwe zabezpieczenia i przekroje przewodów. Moim zdaniem warto od razu wyrabiać nawyk liczenia zarówno rezystancji zastępczej, jak i rozkładu mocy, bo w realnych układach awionicznych mamy dużo bardziej rozbudowane sieci, ale opierają się dokładnie na tych samych zasadach. Dobrą praktyką w technice jest też zawsze sprawdzić wynik „na zdrowy rozsądek”: tu napięcie 28 V i rezystancja 28 Ω dają prąd 1 A, więc moc rzędu kilkudziesięciu watów jest jak najbardziej logiczna.
Żeby dobrze zrozumieć to zadanie, trzeba spokojnie przeanalizować topologię obwodu i nie iść na skróty z liczbami. Na schemacie mamy źródło 28 V, rezystor R1 w szeregu oraz dwa rezystory R2 i R3 połączone równolegle. Typowy błąd polega na traktowaniu wszystkich rezystorów jakby były połączone szeregowo i zwykłym dodaniu ich wartości. Gdy ktoś zsumuje 14 Ω + 28 Ω + 28 Ω, dostaje 70 Ω, a potem liczy prąd i moc. To prowadzi do zaniżonej mocy, bo połączenie równoległe zawsze zmniejsza rezystancję zastępczą, a nie ją zwiększa. Innym błędnym podejściem jest przyjęcie, że moc liczymy tylko na jednym z rezystorów lub na części układu, a nie na całym obwodzie, co może prowadzić do rezultatów typu 1,8 W czy 14 W. Takie wartości sugerują, że ktoś użył wzoru P = I²·R lub P = U²/R, ale dla niewłaściwego fragmentu układu, np. tylko dla R1 albo tylko dla jednej gałęzi, zamiast dla całości, o którą pyta zadanie. Zdarza się też, że ktoś próbuje bezpośrednio podstawiać do wzoru P = U²/R pojedynczą rezystancję 28 Ω, ignorując fakt, że to napięcie 28 V nie odkłada się na jednym rezystorze, tylko na całym szeregowym połączeniu R1 i gałęzi równoległej. Wtedy wynik liczbowo może wyglądać „ładnie”, ale fizycznie nie odpowiada mocy w całym obwodzie. Poprawna droga to najpierw policzyć rezystancję zastępczą połączenia równoległego R2 i R3, następnie dodać ją do R1, żeby otrzymać rezystancję całkowitą. Dopiero potem, korzystając z prawa Ohma, wyznaczamy prąd i moc całkowitą. W praktyce technicznej, szczególnie w instalacjach 28 V DC w lotnictwie, takie pomyłki mogą skutkować złym doborem bezpieczników lub przekrojów przewodów. Dlatego dobrą praktyką jest zawsze narysować sobie uproszczony schemat z rezystancją zastępczą i sprawdzić, czy wynik ma sens: połączenie równoległe dwóch jednakowych rezystorów nigdy nie może dać większego oporu niż pojedynczy, a całkowita moc w obwodzie zasilanym stałym napięciem rośnie, gdy maleje rezystancja zastępcza. To są takie proste, ale bardzo ważne zasady, które z mojego doświadczenia ratują przed wieloma głupimi błędami.