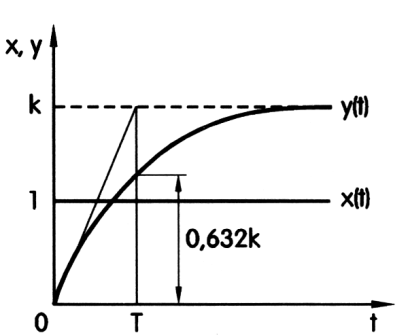
Na wykresie widać klasyczną odpowiedź skokową członu inercyjnego pierwszego rzędu. Wejście x(t) to skok jednostkowy (w tym rysunku od 0 do 1), a wyjście y(t) narasta wykładniczo i asymptotycznie zbliża się do wartości k. Kluczowy szczegół to zaznaczenie chwili T, dla której odpowiedź osiąga około 0,632·k – to dokładnie definicja stałej czasowej członu inercyjnego pierwszego rzędu. Dla takiego członu o transmitancji G(s)=k/(Ts+1) odpowiedź na skok jednostkowy ma postać y(t)=k·(1−e^{−t/T}). Jeśli wstawisz t=T, dostajesz y(T)=k·(1−e^{−1})≈0,632·k, czyli dokładnie to, co jest na rysunku. Moim zdaniem to jeden z tych wykresów, które dobrze jest po prostu „mieć w głowie”, bo pojawia się wszędzie: w elektronice (filtr RC, odpowiedź wzmacniacza z ograniczonym pasmem), w automatyce (model prostego układu cieplnego, opóźnienie inercyjne siłowników), ale też w typowych czujnikach stosowanych w lotnictwie. W praktyce, gdy analizujesz np. powolną reakcję wskaźnika lub systemu pomiarowego, patrzysz właśnie na jego człon inercyjny i jego stałą czasową – im większe T, tym wolniejszy układ i bardziej „mułowata” reakcja. Dobra praktyka w projektowaniu torów pomiarowych i sterowania jest taka, żeby znać stałe czasowe kluczowych elementów i świadomie dobierać filtry, wzmacniacze i algorytmy tak, by cały tor miał akceptowalną dynamikę. W diagnostyce też często z odpowiedzi skokowej szacuje się T i k, żeby zbudować prosty model obiektu i sprawdzić, czy zachowuje się zgodnie z dokumentacją producenta.
Na rysunku pokazano odpowiedź skokową typowego członu inercyjnego pierwszego rzędu, ale łatwo tu pomylić ją z innymi podstawowymi blokami. Intuicyjnie wielu osobom wydaje się, że skoro wyjście rośnie mniej więcej liniowo na początku, to może to być człon proporcjonalny, opóźniający albo całkujący. Warto więc uporządkować sobie, jak te odpowiedzi naprawdę wyglądają. Człon proporcjonalny reaguje na skok natychmiastowo: jeśli wejście zmienia się skokowo z 0 do 1, to wyjście przeskakuje od razu z 0 do k. Na wykresie nie byłoby żadnego „narastania w czasie”, tylko pionowa zmiana. Brak jest jakiejkolwiek stałej czasowej – tor jest idealnie szybki, co oczywiście w realnych układach jest tylko przybliżeniem, ale model matematyczny właśnie tak to opisuje. Człon opóźniający (czysty czas martwy) też wygląda inaczej: przez pewien czas po skoku wejścia wyjście w ogóle nie reaguje (utrzymuje się na 0), a dopiero po czasie opóźnienia pojawia się skok lub dalsza dynamika związana z kolejnymi elementami. Na rysunku nie ma takiego „martwego” odcinka, odpowiedź zaczyna rosnąć od t=0, więc nie jest to czyste opóźnienie. Z kolei człon całkujący na skok wejściowy daje odpowiedź liniową w czasie: y(t) rośnie wprost proporcjonalnie do t, bez górnego ograniczenia, po prostu linia prosta o stałym nachyleniu. Tymczasem tu widzimy przebieg wykładniczo zbliżający się do pewnej stałej wartości k, z wyraźnie zaznaczoną wartością 0,632·k w chwili T. To typowy błąd myślowy: mylenie krzywej wykładniczej z prostą linią, zwłaszcza w pierwszej fazie narastania. W praktyce inżynierskiej rozróżnienie tych odpowiedzi jest kluczowe przy analizie torów pomiarowych i układów regulacji – inne jest zachowanie filtru inercyjnego, inne integratora, a jeszcze inne samego wzmocnienia czy opóźnienia czasowego. Dobra praktyka to zawsze patrzeć na: czy jest wartość ustalona, czy jest czas martwy, czy przebieg jest liniowy czy wykładniczy. Wtedy takie zadania przestają być podchwytliwe.