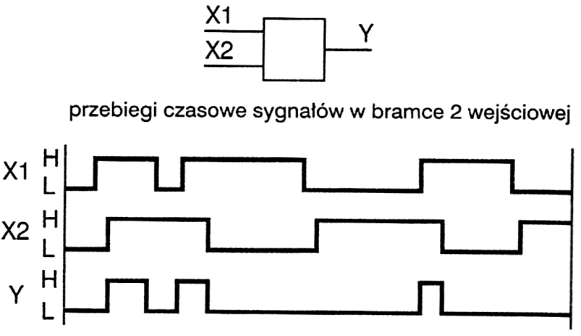
Poprawnie wybrałeś bramkę AND – dokładnie taki charakter mają pokazane przebiegi czasowe. Wyjście Y jest w stanie wysokim tylko wtedy, gdy jednocześnie oba sygnały wejściowe X1 i X2 są w stanie H. W każdym przedziale czasu, kiedy chociaż jedno z wejść spada do L, wyjście natychmiast też przechodzi w L. To jest klasyczna definicja funkcji logicznej iloczynu: Y = X1 · X2. Na rysunku widać, że momenty, w których Y jest wysokie, pokrywają się dokładnie z fragmentami, gdzie oba wejścia są wysokie – ani wcześniej, ani później, bez żadnego „odwracania” czy sumowania. W praktyce takie bramki są fundamentem całej logiki sterującej w systemach awionicznych i instalacjach pokładowych. Typowy przykład: warunek załączenia jakiegoś urządzenia musi spełniać kilka kryteriów naraz, np. zasilanie OK, sygnał z czujnika poprawny i brak sygnału ostrzegawczego. W najprostszej realizacji robi się z tego właśnie iloczyn logiczny, czyli zestaw bramek AND. Jeśli którykolwiek warunek bezpieczeństwa nie jest spełniony (czyli logiczne 0), wyjście układu AND natychmiast spada do 0 i urządzenie nie dostaje sygnału „włącz”. Moim zdaniem bardzo ważne jest, żeby odruchowo kojarzyć: AND = wszystkie warunki naraz. W standardowych rodzinach TTL czy CMOS bramki AND występują w wielu odmianach (2-, 3-, 4-wejściowe), a projektując układ warto pamiętać o czasach propagacji i dopuszczalnym obciążeniu wyjścia, żeby nie doprowadzić do błędnych stanów przejściowych. W dokumentacjach serwisowych samolotów często logika sterowania jest opisana właśnie symbolami AND, OR, NOT, więc dobre rozumienie działania tej podstawowej bramki bardzo ułatwia czytanie schematów i diagnozowanie usterek.
Na rysunku widać typowe przebiegi iloczynu logicznego, ale łatwo się tu pomylić, bo wszystkie wymienione bramki są do siebie wizualnie podobne w symbolice blokowej. Klucz leży w analizie relacji między X1, X2 a Y w czasie. Wyjście Y jest wysokie tylko wtedy, gdy jednocześnie oba wejścia są wysokie. W żadnym momencie nie pojawia się sytuacja, że wystarczy jedno wejście w stanie H, żeby Y było H – to od razu eliminuje bramkę OR. Dla bramki OR sumy logicznej wystarczyłoby, że X1 albo X2 jest wysokie, wtedy Y byłoby wysokie przez znacznie dłuższe odcinki czasu niż na rysunku. To jest dość częsty błąd: intuicyjnie ktoś widzi, że sygnał wyjściowy „pojawia się, gdy coś jest na wejściu” i od razu myśli o OR, bez sprawdzenia współwystępowania obu sygnałów. Bramka NOT też tu nie pasuje z definicji, bo NOT ma tylko jedno wejście i po prostu odwraca stan: H na wejściu daje L na wyjściu i odwrotnie. Na wykresie mamy dwa niezależne przebiegi wejściowe X1 i X2, więc już sama liczba wejść wyklucza inwerter. Dodatkowo kształt Y w ogóle nie jest prostym odwróceniem żadnego z wejść, tylko wynika z ich kombinacji. Kolejna pułapka to bramka NAND. NAND jest zanegowanym AND, czyli Y = ¬(X1 · X2). Logicznie działa odwrotnie: wyjście jest niskie tylko wtedy, gdy oba wejścia są wysokie; w pozostałych przypadkach jest wysokie. Gdyby na rysunku była bramka NAND, odcinki, w których oba wejścia są H, powinny odpowiadać stanowi L na wyjściu, a jest dokładnie odwrotnie. Z mojego doświadczenia sporo osób myli AND z NAND, bo na schematach różnią się tylko małym kółeczkiem na wyjściu, a przy analizie czasówek łatwo to przeoczyć. Typowy błąd myślowy przy takich zadaniach polega na patrzeniu tylko na fragment przebiegu, a nie na całość. Dobra praktyka jest taka, żeby krok po kroku przejść po osi czasu i dla każdego odcinka sprawdzić wszystkie kombinacje wejść oraz wynikającą z definicji funkcję logiczną. Wtedy widać jasno, że tylko zachowanie charakterystyczne dla bramki AND idealnie zgadza się z pokazanym przebiegiem Y, natomiast OR, NOT i NAND dałyby zupełnie inne relacje między H i L na wyjściu.