Kwalifikacja: TLO.01 - Wykonywanie obsługi technicznej wyposażenia awionicznego i elektrycznego statków powietrznych
Zawód: Technik awionik
Kategorie: Pomiary i czujniki Podstawy fizyki lotniczej
Rysunek przedstawia prędkość lotu samolotu określoną na podstawie zapisu rejestratora lotu. Jaką drogę przebył samolot w przedziale czasu [6s, 8s]?
Odpowiedzi
Informacja zwrotna
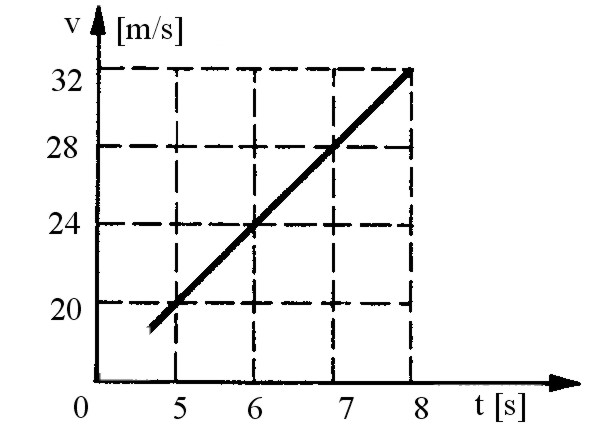
Klucz do tego zadania to zrozumienie, że na wykresie v(t) (prędkość w funkcji czasu) droga jest równa polu pod wykresem. Nie liczymy tu żadnych „magicznych” wzorów z pamięci, tylko patrzymy na geometrię: w przedziale od 6 s do 8 s wykres jest linią prostą rosnącą, więc pole pod nią to po prostu pole trapezu. Z wykresu widać, że w chwili t = 6 s prędkość samolotu wynosi 24 m/s, a w chwili t = 8 s – 32 m/s. Czas trwania analizowanego odcinka to 2 s. Stosujemy więc klasyczny wzór na drogę przy ruchu jednostajnie zmiennym (albo, jak kto woli, na pole trapezu): s = ((v1 + v2)/2) · Δt = ((24 m/s + 32 m/s)/2) · 2 s = (56/2) · 2 = 28 · 2 = 56 m. Dlatego odpowiedź 56 m jest jedyną poprawną. W praktyce lotniczej dokładnie tak samo interpretuje się logi rejestratorów parametrów lotu czy zapisy FDR – z wykresów prędkości, wysokości czy przyspieszeń wyciąga się wnioski o przebytej drodze, profilu wznoszenia czy obciążeniach. Moim zdaniem warto tu zapamiętać dwie rzeczy: po pierwsze, zawsze patrzymy, jaka wielkość jest na osi pionowej i poziomej; po drugie, jeśli mamy wykres prędkość–czas, to droga = pole pod wykresem. To jest standardowa, podręcznikowa metoda stosowana nie tylko w fizyce szkolnej, ale też w analizie danych eksploatacyjnych w lotnictwie, w diagnostyce i przy ocenie zgodności parametrów lotu z procedurami. Technicy i inżynierowie, którzy pracują z systemami awionicznymi i rejestratorami, na co dzień korzystają z takich prostych zależności, tylko często w znacznie bardziej skomplikowanej, cyfrowej formie. Ale fundament jest dokładnie ten sam, co w tym zadaniu.