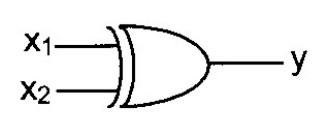
Poprawnie rozpozniono bramkę EXOR (exclusive OR). Widać to od razu po tabeli prawdy: wyjście y ma stan 1 dokładnie wtedy, gdy sygnały na wejściach x1 i x2 są różne. Dla kombinacji 0–0 i 1–1 na wyjściu jest 0, a dla 0–1 i 1–0 jest 1. To jest klasyczna definicja funkcji XOR: y = x1 ⊕ x2, którą można też zapisać jako y = x1·¬x2 + ¬x1·x2. Dodatkowo symbol graficzny ma charakterystyczny „podwójny łuk” po stronie wejść – to standardowe oznaczenie bramki EXOR zgodnie z typową notacją stosowaną w elektronice cyfrowej. Moim zdaniem warto zapamiętać, że EXOR to po prostu „detektor różnicy” logicznej. W praktyce używa się go do porównywania sygnałów (komparatory jedno- i wielobitowe), do generowania bitu parzystości w transmisji danych, w sumatorach binarnych jako element realizujący sumę bez przeniesienia, a także w prostych układach szyfrujących (operacje XOR w kryptografii i kodowaniu). W awionice i systemach pokładowych podobne bramki są częścią większych układów: komputerów misji, FMS, systemów testujących poprawność transmisji w magistralach danych (np. ARINC, MIL‑STD‑1553), czy w układach nadzorujących zgodność sygnałów z redundantnych czujników. Dobrą praktyką w projektowaniu układów cyfrowych jest sprawdzanie zarówno tabeli prawdy, jak i symbolu graficznego, bo w dokumentacji serwisowej czy schematach instalacji pokładowych często pojawia się tylko jeden z tych elementów. Znając charakterystyczny kształt bramki EXOR oraz jej tabelę prawdy, łatwiej potem analizować schematy, diagnozować usterki i rozumieć działanie bardziej złożonych bloków logicznych w systemach elektronicznych statku powietrznego.
Tabelę prawdy w zadaniu warto przeczytać bardzo uważnie, bo to ona jednoznacznie definiuje typ bramki. Wyjście y jest równe 1 tylko wtedy, gdy na wejściach x1 i x2 występują różne stany: dla kombinacji 0–1 i 1–0. Gdy oba wejścia są jednakowe (0–0 lub 1–1), na wyjściu pojawia się 0. Taki przebieg zależności przeczy zachowaniu typowej bramki AND, która daje 1 wyłącznie przy 1–1, więc tu wyraźnie tego nie ma. Z kolei bramka NAND jest negacją AND, czyli jej wyjście jest 0 tylko przy 1–1, a w pozostałych przypadkach 1. W tabeli z zadania przy 0–0 mamy 0, a przy 1–1 także 0, więc nie pasuje ani AND, ani NAND. Częsty błąd polega na tym, że ktoś patrzy tylko na dwa środkowe wiersze tabeli (0–1 i 1–0) i widzi tam jedynki, po czym automatycznie kojarzy to z funkcją OR lub z jej negacjami. Jednak zwykła bramka OR miałaby 1 również przy 1–1, a tutaj przy 1–1 jest wyraźnie 0. NOR to z kolei negacja OR, więc dawałaby 1 tylko dla 0–0, a w pozostałych przypadkach 0. Tabelka z zadania jest więc dokładnym przeciwieństwem takiego zachowania dla części kombinacji. W efekcie ani NOR nie pasuje do podanych wartości, ani żaden prosty wariant negacji wejść nie doprowadzi nas do zgodności. Właściwe podejście polega na rozpoznaniu charakterystycznego wzorca: wyjście równe 1 wtedy, gdy liczba jedynek na wejściach jest nieparzysta. Dla dwóch wejść oznacza to dokładnie sytuacje 0–1 i 1–0. To jest definicja bramki EXOR. Dodatkowo symbol graficzny na rysunku ma dodatkowy, drugi łuk po stronie wejściowej – to standardowy znak, że nie jest to zwykła OR, tylko właśnie XOR. Z mojego doświadczenia wynika, że mylenie XOR z OR lub NOR wynika z pośpiechu i patrzenia tylko na fragment tabeli prawdy, bez sprawdzenia wszystkich kombinacji. W pracy z układami cyfrowymi, szczególnie w awionice i elektronice pokładowej, dobra praktyka to zawsze pełne przeanalizowanie tabeli prawdy oraz symbolu z dokumentacji, zanim wyciągnie się wniosek o rodzaju bramki.