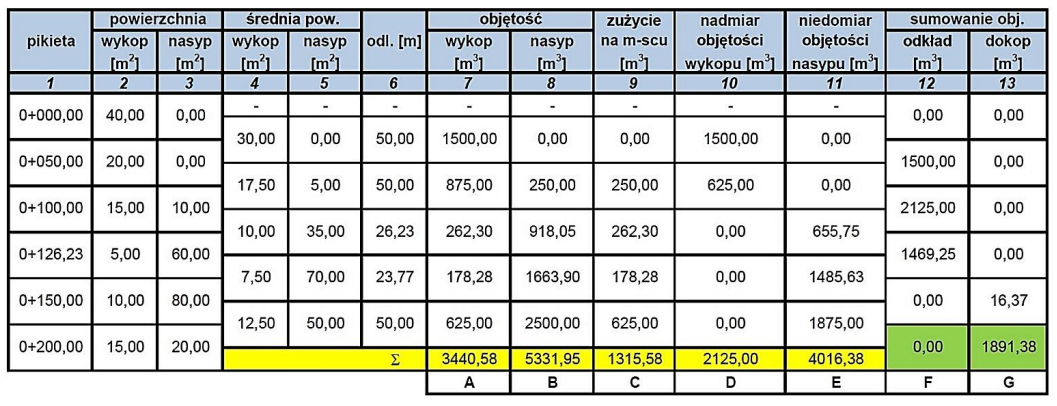
Poprawna odpowiedź to 10,00 m2, ponieważ średnia powierzchnia wykopów między km 0+100,00 a km 0+126,23 obliczana jest na podstawie wartości powierzchni wykopów dla tych pikiet. W danych z tabeli wartości te wynoszą 15,00 m2 dla km 0+100,00 oraz 5,00 m2 dla km 0+126,23. Aby uzyskać średnią, należy zsumować te wartości i podzielić przez ich liczbę, co daje (15,00 m2 + 5,00 m2) / 2 = 10,00 m2. Tego rodzaju obliczenia są kluczowe w projektach budowlanych i inżynieryjnych, gdzie precyzyjne określenie powierzchni robót jest istotne dla oszacowania kosztów oraz planowania zasobów. Zgodnie z normami inżynieryjnymi, poprawne obliczenie średnich wartości jest niezbędne do uzyskania rzetelnych danych do dalszych analiz i planowania, na przykład w kontekście zarządzania projektami budowlanymi. Warto również zauważyć, że umiejętność wykonywania takich obliczeń jest fundamentalna w pracy inżyniera i powinna być regularnie ćwiczona, aby zapewnić dokładność i spójność w realizacji projektów.
Niepoprawne odpowiedzi, takie jak 15,00 m2, 20,00 m2 oraz 35,00 m2, wskazują na typowe błędy związane z obliczeniami średniej wartości. Często w obliczeniach średnich pojawia się nieporozumienie dotyczące procesu sumowania i dzielenia przez odpowiednią liczbę elementów. Na przykład, wybierając 15,00 m2, można zakładać, że jest to właściwa wartość, ponieważ jest to jedna z wartości podanych w tabeli. Jednakże ujęcie tylko jednego pomiaru i ignorowanie drugiego prowadzi do błędnych wniosków. W przypadku 20,00 m2 oraz 35,00 m2 występuje podobny problem – te wartości nie są zgodne z rzeczywistymi danymi, co również może wynikać z nieprawidłowego zrozumienia, jak obliczać średnią z dwóch pomiarów. Ważne jest, aby zrozumieć, że średnia arytmetyczna wymaga uwzględnienia wszystkich wartości, co w tym przypadku oznacza zsumowanie 15,00 m2 i 5,00 m2, a następnie podzielenie wyniku przez dwa. Dobre praktyki w inżynierii wymagają dokładności i systematyczności w podejściu do danych, a także umiejętności krytycznego myślenia, aby unikać pułapek wynikających z powierzchownego analizowania danych. Aby uniknąć podobnych błędów, warto regularnie ćwiczyć obliczenia oraz analizować różne rodzaje danych, co pozwoli na lepsze zrozumienie i interpretację wyników w praktyce.