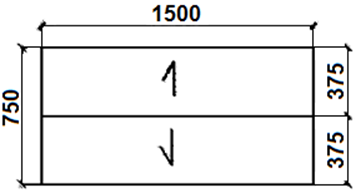
Obliczenie powierzchni dachu na podstawie podanych wymiarów to świetny przykład praktycznego zastosowania matematyki w budownictwie. Na rysunku widzimy dwuspadowy dach o prostokątnym rzucie, gdzie długość wynosi 15 metrów, a szerokość połaci – 7,5 metra. Całościowa powierzchnia jednej połaci to po prostu iloczyn tych dwóch wartości, więc 15 m × 7,5 m = 112,5 m². To klasyczne zadanie, które często pojawia się podczas przygotowania kosztorysów czy zamawiania materiałów dachowych. W praktyce, zawsze warto doliczyć zapas materiału (np. na zakłady lub ewentualne docinki), ale obliczenia bazowe opieramy właśnie na tego typu prostych wzorach geometrycznych. Z mojego doświadczenia wynika, że takie wyliczenia są fundamentem pracy każdego wykonawcy – bez tego ani rusz! Warto pamiętać, że każde odchylenie od standardowych wymiarów wymaga ponownego przeliczenia, a przy bardziej skomplikowanych kształtach dachu (np. mansardowych czy wielospadowych) dochodzą dodatkowe trudności. Fachowcy zawsze podkreślają, by bazować na rzeczywistych wymiarach z projektu i stosować się do norm branżowych, takich jak PN-EN 1991-1-4. W codziennej pracy taka wiedza pozwala uniknąć kosztownych błędów, a w testach – prawidłowo rozwiązywać zadania.
Zadania dotyczące obliczania powierzchni dachów potrafią zaskoczyć, zwłaszcza gdy nie uwzględni się wszystkich istotnych wymiarów lub źle zinterpretuje się rysunek techniczny. W tym przypadku pojawia się kilka typowych błędów myślowych. Często spotykam się z sytuacją, w której ktoś myli powierzchnię rzutu dachu (czyli obrys na poziomie gruntu) z rzeczywistą powierzchnią połaci dachowej. Rzut, choć przydatny, nie uwzględnia faktycznego pochylenia połaci, co przy innych typach dachów może znacząco wpłynąć na końcowy wynik. Z kolei zaokrąglanie wymiarów lub nieuwzględnienie wszystkich boków prostokąta prowadzi do przeszacowania lub niedoszacowania wyniku – to chyba najczęstszy błąd u początkujących. Zdarza się też, że uczniowie zapominają przeliczyć jednostki albo mnożą szerokość przez sumę wysokości obu połaci, co przy tym projekcie nie ma uzasadnienia, bo każda połać liczona jest osobno, a długość dachu wynosi 15 metrów, szerokość pojedynczej połaci to 7,5 metra, więc całość daje 112,5 m². Pomyłki wynikają też z nadmiernego pośpiechu lub nieuwagi przy odczytywaniu rysunku – dlatego zawsze warto dwa razy sprawdzić, czy używamy poprawnych danych. Branżowe standardy wyraźnie wskazują, że precyzyjne obliczanie powierzchni jest bazą do dalszych etapów planowania – zarówno pod kątem materiałów, jak i bezpieczeństwa konstrukcji. Właściwe podejście do takich zadań to nie tylko umiejętność liczenia, ale też rozumienie, skąd biorą się wartości w projekcie i czemu nie warto ich upraszczać na siłę.