Oblicz objętość wykopanego gruntu podczas wykonania 100 m przekopu o przekroju jak na rysunku, pomijając wykonanie rowów bocznych.
A. 1 920 m³
B. 4 240 m³
C. 2 820 m³
D. 2 440 m³
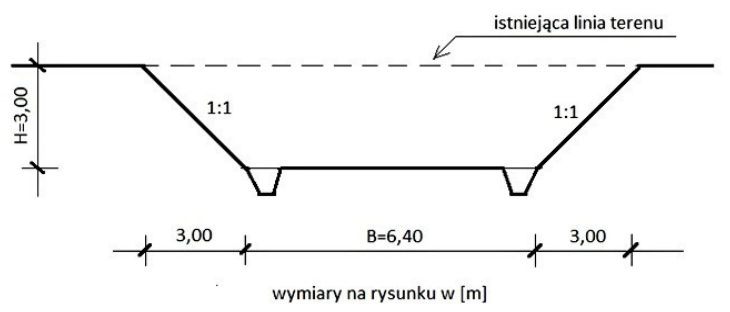
Odpowiedź 2820 m³ jest jak najbardziej poprawna! To wynik, który otrzymujemy, licząc objętość wykopanego gruntu. Mamy wykop, który ma 100 m długości i kształt trapezu, więc używamy wzoru na pole trapezu: P = (a + b) * h / 2. Tu a i b to długości podstaw, a h to wysokość wykopu. Po wyliczeniu pola trapezu multiplikujemy je przez długość wykopu, żeby dostać całkowitą objętość. W budownictwie takie obliczenia są mega ważne, bo dokładne określenie objętości jest kluczowe do planowania transportu materiałów i kosztów budowy. Na przykład, w projektowaniu fundamentów budynków trzeba dobrze obliczyć, ile gruntu się wykopie, żeby dobrać odpowiednie metody budowlane. No i znajomość geometrii, zwłaszcza trapezów, naprawdę pomaga przy ocenie stabilności wykopów, co jest istotne z perspektywy przepisów budowlanych, jak Eurokod 7 dotyczący geotechniki.
Wybór innej odpowiedzi może wynikać z różnych błędów w obliczeniach albo w rozumieniu geometrii. Na przykład, jeśli źle użyjesz wzoru na pole trapezu, to możesz źle obliczyć objętość. Czasami ludzie zapominają uwzględnić odpowiednie wymiary, jak długości podstaw trapezu czy wysokość, co może prowadzić do błędów. Inny typowy problem to pomylenie jednostek miary, co też może skutkować błędami w obliczeniu objętości. Często osoby rozwiązujące takie zadania nie zwracają uwagi na dokładne wymiary i ich jednostki, co potem wpływa na końcowy wynik. To może też prowadzić do nieporozumień związanych z tym, co to właściwie jest objętość i jak się to stosuje w praktyce. Obliczanie objętości wykopów jest naprawdę ważne w budownictwie, bo błędy mogą podnieść koszty lub opóźnić cały projekt. Zdecydowanie trzeba się upewnić, że dane są poprawne przed przystąpieniem do obliczeń. Ogólnie, znajomość geometrii i umiejętność stosowania wzorów matematycznych to podstawa w inżynierii i planowaniu budów.