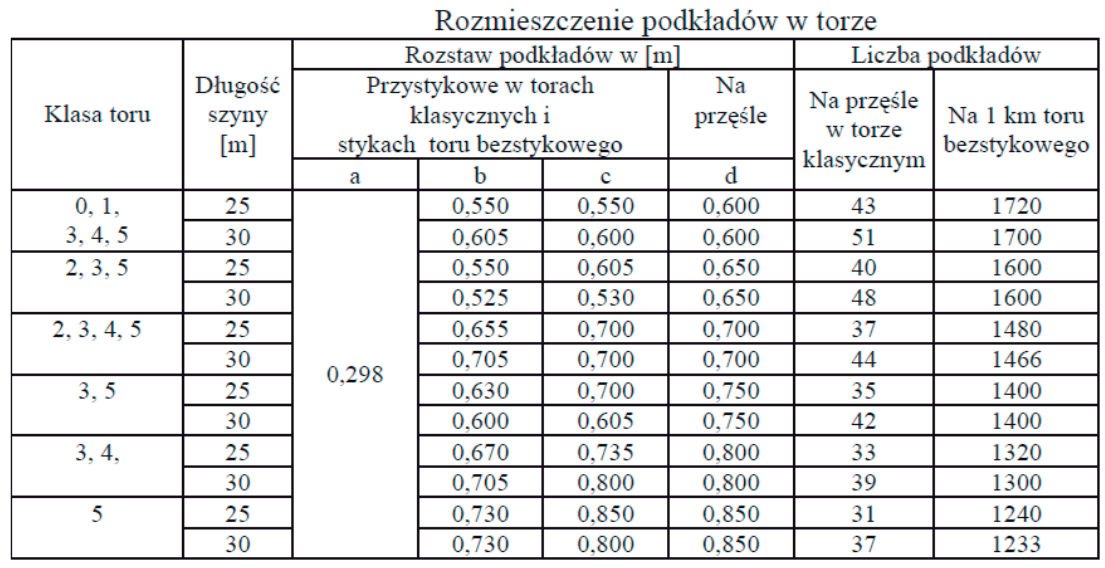
Odpowiedź 51 szt. jest poprawna w kontekście obliczeń dotyczących liczby podkładów w przęśle toru klasycznego klasy 1, o długości 30 m. Zgodnie z tabelą, dla tego typu toru, standardowy rozstaw podkładów wynosi 0,600 m. Aby obliczyć liczbę podkładów, należy podzielić długość przęsła przez rozstaw podkładów, co daje 30 m / 0,600 m = 50. Następnie dodajemy jeden dodatkowy podkład, który jest umieszczany na styku przęseł, co prowadzi do uzyskania wyniku 51 podkładów. W praktyce, uwzględnienie wspólnego podkładu jest kluczowe dla zapewnienia stabilności i ciągłości toru, co jest zgodne z najlepszymi praktykami w budowie infrastruktury kolejowej. Dzięki tym obliczeniom uzyskujemy nie tylko teoretyczne podstawy, ale także praktyczne wskazówki dotyczące realizacji projektów torowych, w których precyzyjne obliczenia są niezbędne dla zapewnienia bezpieczeństwa i efektywności transportu kolejowego.
Wybór innych odpowiedzi, takich jak 37, 43 czy 40 podkładów, może wynikać z niepoprawnego zrozumienia zasad obliczeń dotyczących liczby podkładów w torze klasycznym. Często zdarza się, że osoby podejmujące takie obliczenia mylą się w interpretacji danych dostarczonych przez tabele, co prowadzi do błędnych wyników. Na przykład, wybór 40 sztuk zakładałby, że rozstaw podkładów wynosi 0,750 m, co jest niezgodne z rzeczywistością. Rozstaw 0,600 m jest standardowy i jego zastosowanie w obliczeniach jest kluczowe dla zachowania odpowiedniej liczby podkładów niezbędnych do zapewnienia odpowiedniej nośności i komfortu przejazdu. Błędne podejście do obliczeń może również wynikać z niepełnego uwzględnienia podkładów wspólnych, które są niezbędne w przypadku łączeń przęseł. Ignorowanie tego elementu prowadzi do przyjęcia zaniżonej liczby podkładów, co może wpływać na całą konstrukcję toru oraz jej stabilność. Znajomość dobrych praktyk w zakresie projektowania infrastruktury kolejowej jest niezbędna, aby unikać takich błędów i zapewnić odpowiednią eksploatację systemu kolejowego.