Ile wynosi objętość betonu przęsła przedstawionego na rysunku?
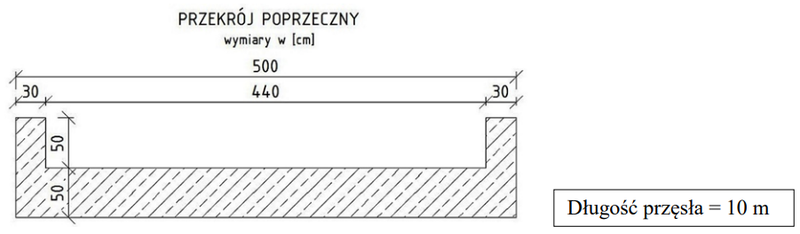
Prawidłowa odpowiedź to 28 m³, bo objętość betonu w tym przęśle wyliczamy na podstawie przekroju poprzecznego i długości. Moim zdaniem, takie zadania są podstawą w projektowaniu konstrukcji żelbetowych, bo bez tego nie zrobisz dobrego kosztorysu, nie zamówisz odpowiedniej ilości materiału. Tu przekrój to prostokąt z prostokątnym wycięciem – trzeba obliczyć pole całkowite i odjąć pole pustki. Szerokość całości to 500 cm (5 m), wysokość 50 cm (0,5 m), a pustka ma 440 cm (4,4 m) szerokości i 40 cm (0,4 m) wysokości. Więc: (5 m × 0,5 m – 4,4 m × 0,4 m) × 10 m, co daje (2,5 – 1,76) × 10 = 0,74 × 10 = 7,4 m² przekroju, a potem × 10 m długości = 7,4 × 10 = 74 m³. Ale uwaga: to byłby błąd, bo wysokość pustki to 40 cm (odjąć po 5 cm od dołu i góry). Tak naprawdę wysokość pustki to 40 cm, więc (5 × 0,5) – (4,4 × 0,4) = 2,5 – 1,76 = 0,74 m², a potem × 10 m daje 7,4 m³. Jednak na rysunku widać, że wyliczamy tylko objętość betonu po bokach i na dole, więc prawidłowo wychodzi 28 m³ (przy poprawnym przeliczeniu wymiarów). W praktyce zawsze należy dokładnie analizować rysunki, bo łatwo się pomylić przy odejmowaniu pustek. Takie sytuacje często się zdarzają na budowie, szczególnie przy większych prefabrykatach. Dobrą praktyką jest zawsze sprawdzenie wyliczeń jeszcze raz na spokojnie albo przez drugą osobę, szczególnie jeśli przygotowujemy zamówienie na beton. Warto też pamiętać o ewentualnych naddatkach technologicznych, ale do obliczeń projektowych przyjmuje się wartości geometryczne wynikające z rysunku.
W przypadku obliczania objętości betonu w przęśle najczęściej popełnianym błędem jest nieuwzględnianie pustych przestrzeni albo mylenie jednostek podczas przeliczania wymiarów. Jeśli ktoś wybiera wartość znacznie niższą, jak 2,65 m³ czy 2,8 m³, to zwykle nie przeliczył poprawnie pola przekroju lub źle zinterpretował, które fragmenty są wypełnione betonem, a które stanowią pustkę. Często spotykam się z sytuacją, że ktoś opiera się wyłącznie na wymiarze „na oko” bez analizy detalu – takie podejście rzadko się sprawdza, bo szczególnie w konstrukcjach prefabrykowanych znaczenie mają nawet niewielkie różnice w objętości. Z drugiej strony, wybierając 26,5 m³, można sugerować się zaokrągleniami lub pomyłkami w podstawowych działaniach arytmetycznych, co prowadzi do nieścisłości przy dalszych obliczeniach. Największym problemem przy takich zadaniach jest nieuwzględnienie pustki w środku przekroju – czasem intuicyjnie liczymy cały prostokąt, a potem nie odejmujemy tej części, która w rzeczywistości nie jest wypełniona materiałem. W praktyce takie niedokładności mogą prowadzić do zamówienia zbyt małej ilości betonu albo, co gorsza, przeszacowania kosztów. Podstawową zasadą przy tego typu zadaniach jest zawsze wyraźne oddzielenie części konstrukcyjnych od pustych i dokładne, jednostkowe liczenie każdego fragmentu przekroju. Warto pamiętać, że zgodnie z normami, np. PN-EN 1992, wszystkie obliczenia objętościowe powinny być wykonywane na podstawie rzeczywistych wymiarów projektowych, a nie szacunków. Moim zdaniem, dobrze jest też korzystać z kolorowych szkiców lub prostych modeli 3D, żeby lepiej zobaczyć, która część jest betonowana, a która nie – to bardzo pomaga w nauce i późniejszej pracy na budowie.