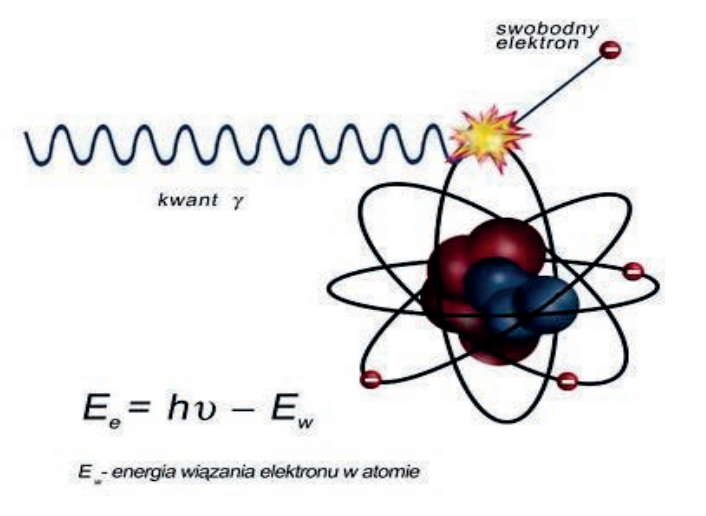
Na rycinie widać klasyczny schemat zjawiska fotoelektrycznego: kwant promieniowania γ (lub X) pada na elektron związany w atomie, przekazuje mu energię i wybija go poza atom jako elektron swobodny. Opis matematyczny Ee = hν − Ew pokazuje, że energia kinetyczna elektronu wybitego (Ee) jest równa energii fotonu (hν) pomniejszonej o energię wiązania elektronu w atomie (Ew). To jest dokładnie definicja efektu fotoelektrycznego, tak jak uczą w fizyce medycznej i w podstawach radiologii. W diagnostyce obrazowej to zjawisko ma ogromne znaczenie przy niższych energiach promieniowania, typowych np. dla mammografii czy zdjęć kostnych – tam dominująca absorpcja w tkankach to właśnie fotoefekt. Moim zdaniem warto zapamiętać, że fotoefekt jest mocno zależny od liczby atomowej Z materiału (z grubsza rośnie jak Z³) – dlatego kości, zawierające dużo wapnia, pochłaniają więcej promieniowania niż tkanki miękkie i wychodzą na zdjęciu jaśniej. W praktyce technika radiologiczna wykorzystuje to przy doborze napięcia kV: niższe kV wzmacnia udział zjawiska fotoelektrycznego, poprawia kontrast tkankowy, ale zwiększa dawkę pochłoniętą. Standardy ochrony radiologicznej i dobre praktyki (np. zasada ALARA) wymagają takiego doboru parametrów, żeby uzyskać wystarczającą jakość obrazu przy jak najmniejszej dawce, czyli rozsądnego kompromisu między udziałem fotoefektu a rozpraszaniem Comptona. Warto też pamiętać, że po wybiciu elektronu w atomie powstaje luka w powłoce, co prowadzi do emisji promieniowania charakterystycznego lub elektronów Augera – to z kolei leży u podstaw działania kontrastów zawierających jod czy gadolin w niektórych technikach obrazowania.
Na ilustracji przedstawiono sytuację, w której pojedynczy foton całkowicie oddaje swoją energię elektronowi związanym w atomie i zanika, a elektron staje się swobodny. Równanie Ee = hν − Ew jednoznacznie opisuje bilans energetyczny dla zjawiska fotoelektrycznego: energia fotonu (hν) jest zużywana na pokonanie energii wiązania elektronu w atomie (Ew), a nadwyżka pojawia się jako energia kinetyczna wybitego elektronu. Częsty błąd polega na myleniu tego schematu z efektem Comptona. W rozproszeniu Comptona foton zderza się z elektronem prawie swobodnym, ale po zderzeniu nadal istnieje foton, tylko o mniejszej energii i zmienionym kierunku. Na rysunkach zwykle widać wtedy dwa promienie: padający i rozproszony, oraz kąt rozproszenia. Tutaj natomiast foton po prostu się "kończy" na atomie, więc nie pasuje to do Comptona. Zjawisko anihilacji dotyczy zupełnie innej sytuacji fizycznej – spotkania elektronu z pozytonem. W wyniku anihilacji materia zamienia się w promieniowanie, powstają zazwyczaj dwa fotony 511 keV lecące w przeciwnych kierunkach. Ten mechanizm jest podstawą działania PET w medycynie nuklearnej, ale na zaprezentowanej rycinie nie ma ani pozytonu, ani przeciwbieżnych fotonów, więc taka interpretacja jest po prostu nie na miejscu. Zjawisko tworzenia par jest jakby odwrotnością anihilacji: wysokoenergetyczny foton w polu jądra zamienia się w parę elektron–pozyton. W schematach widzimy wtedy jądro atomowe oraz dwie przeciwne trajektorie cząstek naładowanych. Tutaj mamy tylko jeden elektron i brak pozytonu, więc również nie pasuje. Typowym błędem myślowym jest patrzenie tylko na słowa "kwant γ" i automatyczne kojarzenie tego z medycyną nuklearną czy PET, bez analizy bilansu energii i liczby cząstek przed oraz po zjawisku. W fizyce medycznej, zgodnie z dobrymi praktykami, zawsze warto patrzeć na to, co dzieje się z fotonem po oddziaływaniu: czy zanika całkowicie (fotoefekt), czy tylko traci część energii (Compton), czy zamienia się w parę cząstek (tworzenie par). Dopiero taka analiza pozwala poprawnie rozpoznać mechanizm na schematach i potem stosować tę wiedzę przy doborze energii wiązki w diagnostyce czy radioterapii.