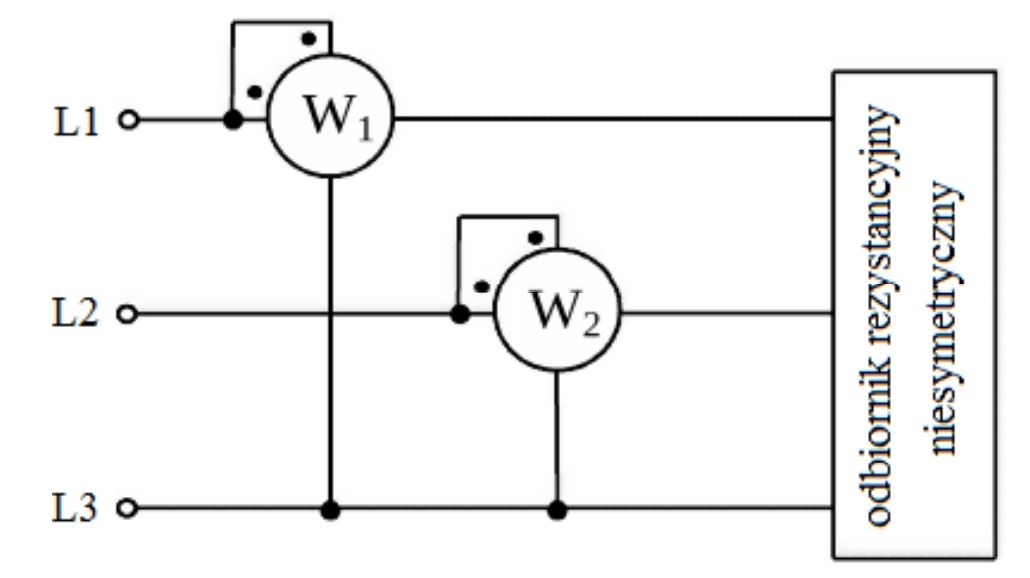
W tym układzie mamy klasyczny trójfazowy pomiar mocy metodą dwóch watomierzy. Odbiornik jest niesymetryczny, ale rezystancyjny, więc pracuje z cos φ ≈ 1 (prąd w fazie z napięciem). Dla takiego przypadku obowiązuje bardzo prosta zasada: moc całkowita odbiornika trójfazowego równa się sumie algebraicznej wskazań obu watomierzy. Czyli liczymy po prostu: P = P1 + P2 = 1000 W + 500 W = 1500 W. To właśnie 1 500 W jest mocą czynną pobieraną przez odbiornik z sieci. Warto zauważyć, że metoda dwóch watomierzy jest standardowo stosowana w praktyce przy pomiarach mocy w sieciach trójfazowych 3‑przewodowych (bez przewodu neutralnego), co opisują m.in. normy z serii PN‑EN 61557 oraz podręczniki z pomiarów elektrycznych. Jeżeli obciążenie jest rezystancyjne, watomierze zwykle pokazują wartości dodatnie i interpretacja jest bardzo prosta – wystarczy zsumować wskazania. W rzeczywistych instalacjach, np. w rozdzielniach zasilających silniki trójfazowe, grzałki trójfazowe czy piece oporowe, technik po prostu odczytuje P1 i P2, dodaje je i ma od razu moc całkowitą zestawu. Moim zdaniem to jedno z bardziej praktycznych narzędzi, bo pozwala szybko sprawdzić, czy odbiornik nie przekracza mocy znamionowej zabezpieczeń albo transformatora zasilającego. Dobrą praktyką jest też porównanie wyniku z mocą obliczeniową instalacji, żeby ocenić rezerwę mocy i ewentualnie dobrać odpowiednie przekładniki prądowe i napięciowe do stałych pomiarów energii.
W zadaniu pokazano układ pomiaru mocy trójfazowej metodą dwóch watomierzy dla odbiornika rezystancyjnego niesymetrycznego. Kluczowy jest tu sposób interpretacji wskazań P1 i P2. W sieci trójfazowej 3‑przewodowej, przy zastosowaniu dwóch watomierzy, moc całkowita P odbiornika równa się sumie algebraicznej wskazań obu przyrządów: P = P1 + P2. Nie ma tu żadnego mnożenia przez współczynnik ani odejmowania, o ile wiemy, że badamy moc czynną i znamy poprawne podłączenie cewek prądowych i napięciowych. Propozycja 500 W wynika zwykle z mylnego założenia, że jeden z watomierzy „trzeba odjąć”, bo odbiornik jest niesymetryczny. To jest typowy błąd: odejmowanie pojawia się tylko wtedy, gdy jedno z wskazań jest ujemne (wskazówka cofa się), co odpowiada dużemu kątu przesunięcia fazowego, np. przy obciążeniu indukcyjnym. W naszym zadaniu oba wyniki są dodatnie, więc ich różnica nie ma sensu fizycznego jako moc całkowita. Wartość 866 W może kojarzyć się z operacjami typu dzielenie przez √3 lub różnymi przeliczeniami między mocą pozorną i czynną. To także jest błędne podejście: tutaj nie liczymy mocy pozornej S ani mocy na fazę, tylko bezpośrednio moc czynną trójfazową, którą metoda dwóch watomierzy daje wprost jako sumę wskazań. Z kolei 2250 W sugeruje próbę sztucznego „przeliczenia” wyników, np. przez pomnożenie jednego z odczytów przez jakiś współczynnik bezpieczeństwa albo intuicyjne dodanie do sumy jeszcze połowy większego wskazania. Z mojego doświadczenia takie wyniki biorą się z mieszania wzorów dla układów jednofazowych i trójfazowych oraz z niepewności, czy do obliczeń brać wartości fazowe, czy międzyfazowe. Dobra praktyka jest prosta: w metodzie dwóch watomierzy, dla sieci trójfazowej 3‑przewodowej, moc całkowita P = P1 + P2, niezależnie od tego, czy odbiornik jest symetryczny czy niesymetryczny. Dopiero dalsze analizy (np. wyznaczanie cos φ z zależności tan φ = √3 (P1 − P2)/(P1 + P2)) wymagają operowania różnicą wskazań. Jeśli pamięta się tę zasadę, unika się większości typowych pomyłek na egzaminach i w praktycznych pomiarach w instalacjach przemysłowych.