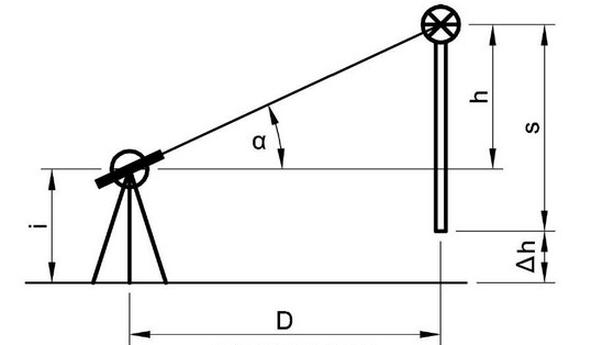
Wzór "D * tgα" jest poprawny do obliczenia przewyższenia h, ponieważ odnosi się do geometrystycznej relacji w trójkącie prostokątnym, gdzie D to długość podstawy, a tgα to tangens kąta α. Wartość tgα definiuje się jako stosunek wysokości h do długości przyprostokątnej D, co można zapisać jako h = D * tgα. W praktyce, stosując ten wzór, możemy dokładnie określić wysokość obiektu lub przewyższenie terenu, co jest kluczowe w geodezji i inżynierii lądowej. Użycie takiego podejścia jest zgodne z dobrymi praktykami w pomiarach geodezyjnych, gdzie precyzja obliczeń jest niezbędna dla uzyskania wiarygodnych wyników. Dodatkowo, znajomość i umiejętność stosowania funkcji trygonometrycznych, jak tangens, są fundamentalne w pracy geodety, ponieważ pozwalają na efektywne przeprowadzenie analizy przestrzennej oraz obliczeń związanych z wysokością i odległością.
Wybór niewłaściwych wzorów do obliczenia przewyższenia h często wynika z niepełnego zrozumienia relacji między kątami a bokami trójkąta prostokątnego. Odpowiedzi takie jak "ctgα/D – s" czy "i + h – s" nie odnoszą się do rzeczywistych związków geometrycznych, które można wykorzystać w analizach trygonometrycznych. Wzór "ctgα/D" wprowadza zamieszanie, ponieważ cotangens kąta nie ma bezpośredniej relacji z obliczaniem wysokości w kontekście pomiaru odległości. Podobnie, wzór "i + h – s" nie ma sensu geometrycznego, ponieważ nie uwzględnia współzależności między długościami boków w trójkącie prostokątnym. W praktyce, błędne podejście do obliczenia przewyższenia może prowadzić do znacznych pomyłek w pomiarach i analizach geodezyjnych. Ponadto, stosowanie wzorów takich jak "D * ctgα" czy "D * tgα" bez zrozumienia kontekstu może prowadzić do poważnych błędów w interpretacji danych. Kluczowe jest, aby przy obliczeniach geodezyjnych zawsze opierać się na właściwych zasadach trygonometrii oraz zasadach geometrycznych, by unikać nieporozumień i zapewnić dokładność oraz wiarygodność wyników pomiarów.