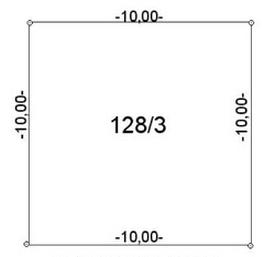
Odpowiedź P = 100 m2 ±0,1 m2 jest poprawna, ponieważ pole powierzchni działki o numerze 128/3, która przyjmuje kształt kwadratu o bokach długości 10,00 m, wynosi dokładnie 100,00 m2. W obliczeniach geodezyjnych, uwzględniając pomiar długości z dokładnością ±5 mm, kluczowe jest przeliczenie błędów pomiarowych na pole powierzchni. W przypadku kwadratu, błąd w pomiarze długości boków przekłada się na błąd w obliczeniu pola powierzchni zgodnie z wzorem P = a^2, gdzie a to długość boku. Wzór na błąd średni pola kwadratu w kontekście błędów pomiarowych boków można zapisać jako: ΔP = 2aΔa. Dla boku 10 m i błędu pomiarowego Δa = 0,005 m (5 mm), otrzymujemy ΔP = 2 * 10 m * 0,005 m = 0,1 m2. Dlatego poprawna odpowiedź uwzględnia zarówno wartość pola, jak i błąd pomiarowy, co odpowiada standardom branżowym w geodezji. W praktyce, takie obliczenia pozwalają na dokładne planowanie przestrzenne oraz minimalizację ryzyka błędów w projektach budowlanych.
Wybór innej odpowiedzi może wynikać z kilku typowych nieporozumień związanych z obliczaniem błędów pomiarowych. Na przykład, odpowiedzi sugerujące błąd średni na poziomie ±0,005 m2 lub ±0,025 m2 nie uwzględniają właściwego przeliczenia błędów wynikających z pomiarów długości na pole powierzchni. Często zdarza się, że osoby dokonujące takich obliczeń nie zdają sobie sprawy, że w przypadku figur płaskich, takich jak kwadrat czy prostokąt, błędy pomiarowe w długości mają znaczny wpływ na obliczane pole. Błąd pomiaru długości boków działa w sposób kwadratowy, co oznacza, że niewielka niepewność w pomiarze długości może prowadzić do znacznego błędu w wyniku końcowym. Wybierając zbyt mały błąd, jak w przypadku ±0,005 m2, można zignorować fakt, że błąd w pomiarze długości, który wynosi ±5 mm, powinien być odpowiednio przeliczony na pole powierzchni. Z kolei wybór błędu ±0,025 m2 przekracza rzeczywistą wartość, co może prowadzić do błędnych wniosków w kontekście geodezyjnym. W geodezji, prawidłowe przeliczenie błędów pomiarowych na obliczenia dotyczące powierzchni jest kluczowe dla zapewnienia wiarygodności wyników oraz ich praktycznego zastosowania w planowaniu przestrzennym i projektowaniu. Dbałość o dokładność pomiarów oraz ich odpowiednie interpretowanie jest niezbędne, aby unikać potencjalnych strat w projektach budowlanych.