Współrzędne punktu P, obliczone na podstawie danych zamieszczonych na szkicu z pomiaru ortogonalnego, wynoszą
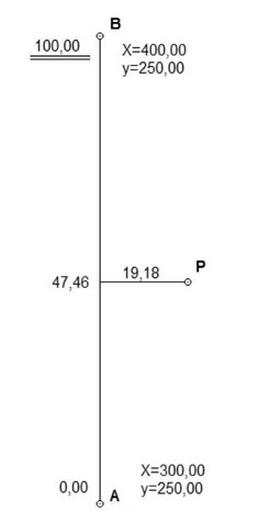
Poprawna odpowiedź wskazuje współrzędne punktu P wynoszące XP = 347,46 m oraz YP = 269,18 m, co jest wynikiem dokładnych obliczeń opartych na pomiarach ortogonalnych. W praktyce, aby uzyskać te współrzędne, dodajemy odległości pomiarowe do współrzędnych punktu wyjściowego A. W przypadku kierunku X, dodajemy odległość AP w poziomie, natomiast w kierunku Y dodajemy odległość AP w pionie. Taki sposób obliczeń jest zgodny z metodami geodezyjnymi, gdzie precyzyjne ustalanie lokalizacji punktów ma kluczowe znaczenie dla jakości pomiarów. Znalezienie współrzędnych punktu P jest istotne w kontekście dalszych prac geodezyjnych, takich jak mapowanie, projektowanie czy roboty budowlane. Przykładem zastosowania tej wiedzy jest tworzenie map topograficznych, gdzie precyzyjne współrzędne są fundamentalne dla przedstawienia terenu, a także dla realizacji projektów budowlanych, które wymagają dokładności w lokalizacji obiektów. Zrozumienie tego procesu pozwala na lepsze planowanie i podejmowanie decyzji w projektach inżynieryjnych.
Wybór niepoprawnych współrzędnych punktu P może wynikać z kilku typowych błędów koncepcyjnych w obliczeniach geodezyjnych. Często myli się kierunki pomiaru, co prowadzi do błędnego dodawania odległości. Na przykład, w sytuacji gdy współrzędne X są błędnie obliczane, może to być skutkiem pomyłki w pomiarze odległości lub zastosowania niewłaściwego kierunku. Przykładowo, jeśli do współrzędnej X dodano wartość odległości w kierunku Y, to wynik będzie nieprawidłowy. Ponadto, błędy mogą wynikać z nieprawidłowego zrozumienia zasad dotyczących pomiaru ortogonalnego. Systemy pomiarowe, w których nie uwzględnia się precyzyjnych wartości odległości, mogą prowadzić do poważnych rozbieżności. Zastosowanie nieodpowiednich metod obliczeniowych, a także nieuwzględnienie błędów systematycznych i przypadkowych, przyczynia się do nieprawidłowych wyników. Aby uniknąć takich błędów, istotne jest zrozumienie podstawowych zasad geometrii analitycznej oraz praktyczne zastosowanie dobrych praktyk w pomiarach, takich jak kalibracja instrumentów i dokładne planowanie kolejności pomiarów. Właściwe podejście do obliczeń oraz uwzględnienie kontekstu wszystkich pomiarów są kluczowe dla uzyskania dokładnych i wiarygodnych wyników.