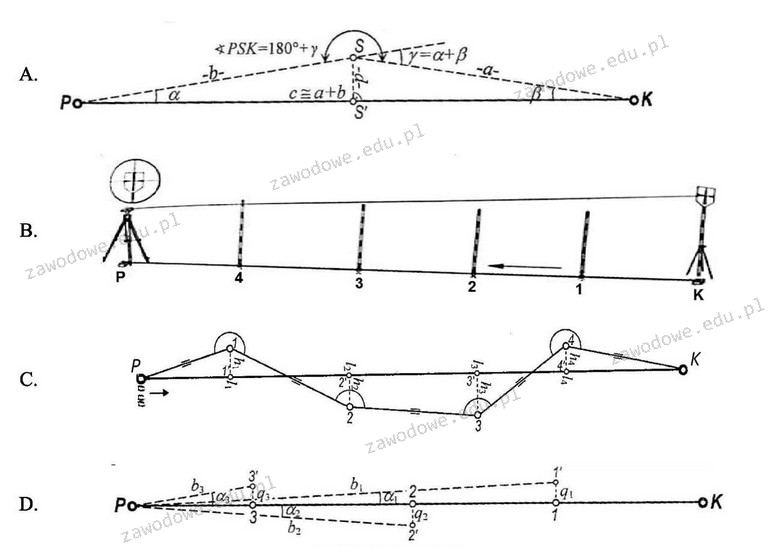
Rysunek A przedstawia metodę tyczenia prostej, która opiera się na użyciu teodolitu, precyzyjnego instrumentu do pomiaru kątów poziomych i pionowych. Umożliwia to dokładne określenie kierunku i długości odcinka, co jest kluczowe w przypadku tyczenia prostych odległych na odległość 3 km. Wysoka precyzja tej metody jest niezbędna, zwłaszcza gdy widoczność pomiędzy punktami jest dobra. Dzięki temu można uniknąć błędów wynikających z nieodpowiednich pomiarów. Przykładowo, w praktyce inżynieryjnej oraz budowlanej, zastosowanie teodolitu pozwala na precyzyjne wytyczanie linii budowlanych, co jest zgodne z normami PN-EN ISO 17123 dotyczącymi pomiarów geodezyjnych. Warto również dodać, że użycie teodolitu jest zgodne z dobrymi praktykami w geodezji, co podnosi jakość i rzetelność realizowanych prac pomiarowych.
Wybór innej odpowiedzi może wynikać z niepełnego zrozumienia metod tyczenia prostych linii w geodezji. Porównując inne rysunki, istotne jest, aby zauważyć, że metody, które nie opierają się na teodolitu, zazwyczaj nie zapewniają wystarczającej precyzji dla długich odcinków, jak 3 km. Na przykład, stosowanie metod opartych jedynie na sznurkach czy prostych pomiarach wzrokowych może prowadzić do błędów w geometrii terenu i wynikającej z tego niezgodności w tyczeniu prostych. Typowym błędem myślowym jest założenie, że dobra widoczność pomiędzy punktami eliminuje potrzebę użycia precyzyjnych instrumentów. W rzeczywistości, nawet w idealnych warunkach, pomiary mogą być zafałszowane przez różnorodne czynniki, takie jak zniekształcenia wizualne, które mogą wystąpić na dużych odległościach. Metody, które nie wykorzystują teodolitu, mogą być bardziej odpowiednie dla krótszych odcinków lub w mniej wymagających warunkach, co może prowadzić do błędnych wniosków o ich zastosowaniu w sytuacji przedstawionej w pytaniu. Dobrym rozwiązaniem w praktyce jest łączenie różnych metod, co jednak wymaga umiejętności oceny ich precyzji oraz odpowiednich warunków zastosowania.