Na podstawie przedstawionego szkicu określ współrzędne prostokątne punktu środkowego S.
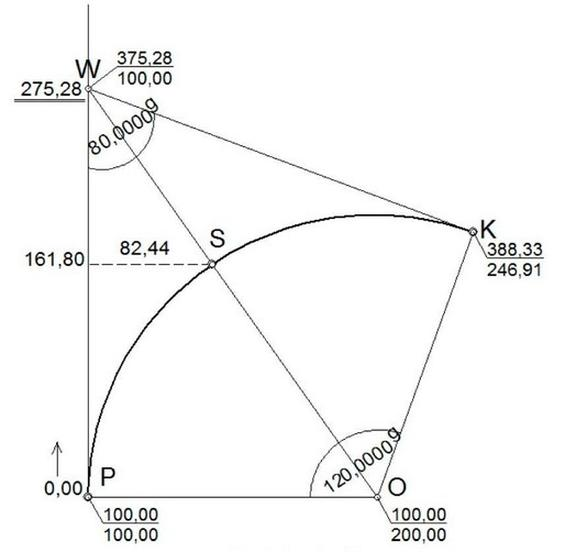
Właściwe współrzędne prostokątne punktu środkowego S wynoszą XS = 261,80 m oraz YS = 182,44 m. Uzyskanie tych wartości wymaga zrozumienia koncepcji układów współrzędnych oraz metod obliczeń związanych z lokalizacją punktów w przestrzeni. W kontekście geodezji, punkty te często wyznaczane są przy użyciu technik pomiarowych, takich jak triangulacja czy pomiar GPS, które zapewniają wysoką dokładność. Przykładowo, w budownictwie i inżynierii lądowej, precyzyjne określenie współrzędnych jest kluczowe dla planowania i realizacji projektów. Warto również zauważyć, że odpowiednie przekształcenia układów odniesienia są istotne w kontekście różnych systemów kartograficznych, co ma zastosowanie w analizach przestrzennych. Zrozumienie, jak obliczać środkowe punkty w oparciu o dane współrzędne, jest niezbędne dla każdego profesjonalisty w dziedzinie geoinformatyki i inżynierii.
Błędne odpowiedzi często wynikają z niepełnego zrozumienia układów współrzędnych oraz metod wyznaczania punktów w przestrzeni. Współrzędne prostokątne są definiowane w kontekście osi X i Y, gdzie każda z nich ma swoją specyfikę i znaczenie. Odpowiedzi, które podają wartości XS = 161,80 m, wskazują na niewłaściwą lokalizację wzdłuż osi X, co może być wynikiem pomyłki w interpretacji przesunięcia punktów na szkicu. Warto zauważyć, że takie błędy mogą wynikać z nieostrożnego odczytu danych, co jest typowym problemem w praktyce geodezyjnej. Ponadto, wybór nieprawidłowych wartości Y dla punktu środkowego może wskazywać na nieprawidłowe przełożenie wymiarów prostopadłych, co jest kluczowe przy określaniu lokalizacji w kontekście projektów budowlanych. Dobrą praktyką jest zawsze weryfikowanie obliczeń oraz ich powiązań z rzeczywistymi pomiarami, co pomaga uniknąć takich pomyłek. Dlatego ważne jest, aby przed podjęciem decyzji o przyjęciu określonych współrzędnych, dokładnie przeanalizować dokumentację techniczną oraz zastosowane metody pomiarowe.