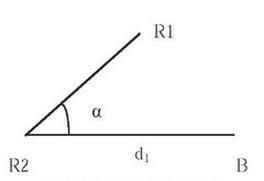
Odpowiedź A jest trafna, bo wzory do obliczania współrzędnych X i Y punktu B, który mierzony jest metodą biegunową, są zgodne z zasadami geodezji. W tej metodzie, współrzędne punktu B oblicza się na podstawie znanych danych, czyli współrzędnych punktu R2 oraz wartości odległości d1 i kąta α. Te wzory, czyli X = X(R2) + d1 * cos(α) i Y = Y(R2) + d1 * sin(α), pozwalają na dokładne określanie pozycji punktów, co jest naprawdę ważne w geodezji i inżynierii. W praktyce, takiego podejścia używa się na przykład w pomiarach terenowych, gdzie zdalne określanie pozycji różnych obiektów jest kluczowe w projektowaniu. Dzięki tym wzorom można być pewnym, że wszystko będzie zgodne z międzynarodowymi standardami w geodezji, co sprawia, że są one przydatne w różnych projektach geodezyjnych.
Niestety, wybór innej odpowiedzi nie jest trafny, bo omija podstawowe zasady obliczeń współrzędnych w metodzie biegunowej. Ta metoda opiera się na tym, że mamy współrzędne znane punktu odniesienia i musimy znać odległość oraz kąt do punktu, który chcemy zmierzyć. Bez precyzyjnych wzorów, które odzwierciedlają te relacje, nie da się dobrze wyliczyć współrzędnych. Inne odpowiedzi mogą wynikać z nieporozumień związanych z rolą różnych parametrów w obliczeniach. Często ludzie mylą kierunek kąta α albo używają złych jednostek miary, co może prowadzić do błędnych wyników. Wzory, które nie pasują do konwencji w geodezji, mogą skutkować sporymi błędami w lokalizacji obiektów, co w praktyce prowadzi do problemów przy realizacji jakichkolwiek budów. Ważne, żeby zrozumieć, że każda metoda pomiarowa ma swoje zasady, których trzeba się trzymać, żeby wyniki były wiarygodne. Używanie złych wzorów nie tylko prowadzi do błędów w obliczeniach, ale może też wiązać się z dużymi stratami finansowymi i opóźnieniami w projektach.