Wzory na obliczenie współrzędnych X i Y punktu kontrolowanego B pomierzonego metodą biegunową (przedstawioną na rysunku) są następujące:
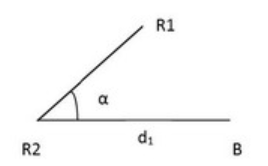
Odpowiedź A jest dobra, bo bazuje na podstawowych wzorach, które używamy w metodzie biegunowej do wyliczania współrzędnych punktu B. Te wzory pomogą nam dokładnie obliczyć współrzędne, mając jakieś znane wartości z punktu odniesienia R2 oraz odległość d1 i kąt α. Na przykład wzór XB = XR2 + d1 * cos(α) daje nam współrzędną X punktu B, bo dodajemy do współrzędnej X punktu R2 wartość, którą przekształca funkcja cosinus, co uwzględnia kąt między tym punktem a kierunkiem geodezyjnym. Analogicznie, wzór YB = YR2 + d1 * sin(α) działa dla współrzędnej Y, gdzie wykorzystujemy funkcję sinus. Takie wzory przydają się w geodezji i kartografii, bo dzięki nim możemy robić precyzyjne mapy i pomiary. Metoda biegunowa jest naprawdę fajna, zwłaszcza w trudnym terenie, gdzie nie da się łatwo zrobić pomiarów.
Wydaje mi się, że wybór tej odpowiedzi nie był najlepszy i wynikał z nieporozumienia z zasadami obliczania współrzędnych w metodzie biegunowej. W tej metodzie ważne jest, żeby zrozumieć, jak współrzędne punktu B są określane w odniesieniu do punktu R2. Często ludzie mylą zasady dotyczące wyliczeń wektora z samymi pomiarami. W rzeczywistości, żeby uzyskać współrzędne punktu kontrolowanego, trzeba uwzględnić kąty i odległości. Jak się tego nie rozumie, to łatwo można podać błędne wartości dla współrzędnych X i Y. Wiele osób nie wie, że funkcje trygonometryczne, takie jak sinus i cosinus, są kluczowe do przekształcenia odległości na współrzędne kartezjańskie. Jeśli pominiesz te funkcje, to nie wyjdzie poprawny wynik i często kończy się na wyborze złej odpowiedzi. W praktyce geodezyjnej metoda biegunowa wymaga precyzyjnych pomiarów kątów i odległości, a złe zrozumienie tego wszystkiego prowadzi do błędów, co będzie miało wpływ na późniejsze analizy. Warto zwrócić uwagę na to, jak ważne jest korzystanie z odpowiednich wzorów w geodezji, bo to jest zgodne z dobrymi praktykami w tej dziedzinie.