Ile m³ gruntu zostanie odspojone z wykopu o długości 200 m i wymiarach przekroju poprzecznego przedstawionego na rysunku?
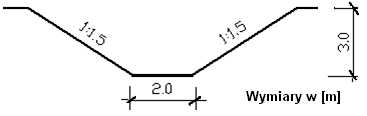
Właściwa odpowiedź wynika z poprawnego obliczenia objętości wykopu o zadanych wymiarach i spadkach skarp. Kluczowe było tu uwzględnienie przekroju poprzecznego, gdzie dno ma szerokość 2 m, głębokość wynosi 3 m, a skarpy są nachylone w stosunku 1:1,5. Najpierw wyznacza się szerokość górną wykopu: do szerokości dna należy dodać dwukrotnie iloczyn głębokości i nachylenia, bo skarpy są po obu stronach (2,0 m + 2 x 3,0 m x 1,5 = 11,0 m). Następnie liczy się pole przekroju poprzecznego – suma prostokąta na dnie i dwóch trapezów skarp. Ja to zawsze robię tak: pole = szerokość dna × głębokość + nachylenie × głębokość² (2,0 × 3,0 + 1,5 × 3,0² = 6,0 + 13,5 = 19,5 m²). Potem już z górki – objętość = długość × pole (200 m × 19,5 m² = 3 900 m³). Takie kalkulacje są na porządku dziennym przy robotach ziemnych, szczególnie przy planowaniu kosztorysu czy harmonogramu. W praktyce inżynierskiej warto korzystać z takich wzorów i zawsze kontrolować wyniki, bo pomyłka może skutkować dużym niedoszacowaniem mas ziemnych, co w terenie jest trudne do naprawienia. Moim zdaniem, precyzyjne liczenie objętości przekopów to podstawa rzetelnej pracy każdego kosztorysanta czy kierownika budowy.
W tego typu zadaniach najczęściej popełnia się błąd przez nieuwzględnienie całego przekroju poprzecznego lub błędne wyliczenie szerokości górnej wykopu. Problem pojawia się zwłaszcza, gdy ktoś zapomina, że nachylenie skarp 1:1,5 sprawia, iż każda skarpa poszerza wykop u góry o długość równą głębokości pomnożonej przez współczynnik nachylenia (czyli 3,0 × 1,5 = 4,5 m z każdej strony). W konsekwencji łatwo zaniżyć pole przekroju, a tym samym objętość – to typowa pułapka, na którą wielu uczniów się łapie. Część osób liczy tylko pole prostokąta na dnie (2,0 × 3,0 = 6,0 m²), ignorując trapezowe skarpy, przez co wynik wychodzi zdecydowanie za mały. Inni mogą mylnie dodawać szerokość dna i sumę długości skarp bez prawidłowego rozplanowania tego na rysunku. No i jeszcze typowy błąd to przeliczenie nachylenia skarpy jako nachylenie pionowe, a nie proporcjonalne względem poziomu – przez co wychodzi np. 2 400 m³ czy 2 100 m³, co nijak się ma do rzeczywistych mas ziemnych. W praktyce budowlanej takie niedoszacowania prowadzą do poważnych problemów z logistyką robót ziemnych, a często też do konfliktów z inwestorem lub wykonawcą. Warto zawsze rozrysować sobie przekrój i krok po kroku policzyć pole – to banał, ale w praktyce najpewniejsza metoda. Z mojego doświadczenia wynika, że dokładność takich obliczeń bardzo doceniają geodeci i kosztorysanci – każdy błąd na tym etapie to później realne pieniądze i czas na budowie.