Ile wynosi objętość gruntu pochodzącego z rowu przydrożnego o wymiarach przekroju poprzecznego podanych na rysunku, jeśli długość tego rowu wynosi 150 m?
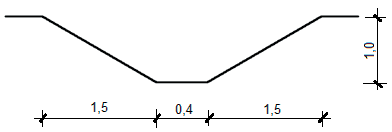
Obliczając objętość gruntu wydobytego z rowu przydrożnego, kluczowe jest prawidłowe określenie pola przekroju poprzecznego i przemnożenie go przez długość rowu. W tym przykładzie mamy klasyczny przekrój trapezowy z dnem o szerokości 0,4 m, skarpami o długości 1,5 m każda i głębokości 1,0 m. Najlepszą praktyką branżową jest rozbicie przekroju na prostokąt (dno) i dwa identyczne trójkąty (skarpowe ściany). Pole prostokąta to 0,4 m × 1,0 m, natomiast trójkąty oblicza się jako 0,5 × 1,5 m × 1,0 m każdy. Suma pól daje 0,4 + 1,5 = 1,9 m². Następnie mnożymy przez długość 150 m: 1,9 × 150 = 285 m³. Ten wynik jest zgodny z praktyką w robotach ziemnych i wytycznymi dotyczącymi pomiarów mas ziemnych, np. według normy PN-B-06050. Tego typu zadania są bardzo przydatne przy szacowaniu kosztów robót, planowaniu wywozu urobku, czy też przy bilansie mas ziemnych na budowie. Moim zdaniem przy tego typu zadaniach warto zawsze szkicować przekrój i rozbijać go na prostsze figury – to ułatwia kalkulacje i pomaga uniknąć typowych błędów, np. złego dodania szerokości lub pominięcia skarp. W praktyce inżynierskiej takie umiejętności pozwalają szybciej rozwiązywać zadania, ale też ułatwiają komunikację z wykonawcami – każdy rozumie, skąd biorą się konkretne liczby.
Obliczając objętość gruntu z wykopu o przekroju złożonym, wielu popełnia błąd, upraszczając pole przekroju poprzecznego do zwykłego prostokąta lub nieuwzględniając wszystkich elementów przekroju. W praktyce, jeśli pominiemy boczne skarpy lub źle zsumujemy szerokości, wynik okaże się o wiele za mały (np. 60 m³) lub odwrotnie – przeszacowany, jeśli zsumujemy szerokości bez uwzględnienia rzeczywistej geometrii, co prowadzi do wartości rzędu 570 m³. Z mojego doświadczenia najczęstszy błąd polega na traktowaniu całego przekroju jako prostokąta o wymiarach 3,4 m × 1,0 m, a następnie przemnażaniu przez długość rowu – to daje zbyt wysoką wartość, bo nie odzwierciedla faktycznej powierzchni przekroju. Z kolei wybranie najniższej wartości świadczy o zignorowaniu skarp, czyli istotnej części masy ziemnej. Praktyka budowlana i normy branżowe, np. PN-B-06050, zalecają rozbijanie przekroju na prostsze figury – prostokąty i trójkąty, co zapewnia dokładność obliczeń. Osoby wybierające odpowiedzi pośrednie (jak 255 m³) zwykle mylą się przy sumowaniu pól trójkątów lub źle zaokrąglają wyniki. Prawidłowa metodologia polega na precyzyjnym obliczeniu pola każdego fragmentu przekroju, a dopiero potem mnożeniu przez długość rowu. To zadanie pokazuje, jak ważne są dokładność, konsekwencja i znajomość podstaw geometrii w pracy technika oraz jak łatwo o pomyłkę, jeśli nie stosujemy się do dobrych praktyk branżowych.