Kwalifikacja: BUD.22 - Organizacja i prowadzenie robót melioracyjnych
Kategorie: Melioracje wodne Budowle wodne Pomiary i kontrola
Projekt przewiduje wykonanie rowu, którego zadaniem będzie przejęcie nadmiaru wody z lokalnych obniżeń terenowych. Rów ma następujące wymiary przekroju poprzecznego:
– szerokość dna – 0,5 m,
– nachylenie skarp – 1:1,5,
– głębokość – 1,2 m.
W którym przypadku szerokość rowu na powierzchni terenu – b jest prawidłowo obliczona?
| Wymiary | A | B | C | D |
|---|---|---|---|---|
| a [m] | 0.5 | 0.5 | 0.5 | 0.5 |
| b [m] | 3.0 | 3.1 | 4.0 | 4.1 |
| h [m] | 1.2 | 1.2 | 1.2 | 1.2 |
Odpowiedzi
Informacja zwrotna
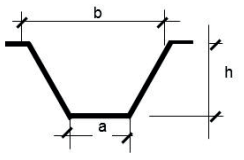
Szerokość rowu na powierzchni terenu oblicza się według wzoru: b = a + 2 * h * m, gdzie a to szerokość dna, h – głębokość rowu, a m to nachylenie skarpy (tu: 1:1,5, czyli m=1,5). Wstawiając wartości z zadania: b = 0,5 + 2 * 1,2 * 1,5 = 0,5 + 2 * 1,8 = 0,5 + 3,6 = 4,1 m. Dokładnie taki wynik daje przypadek D, więc to jest poprawna opcja. Takie obliczenia są standardem przy projektowaniu rowów melioracyjnych, zgodnie z Polską Normą PN-EN 16907-5. Praktyka pokazuje, że niewłaściwe określenie szerokości na powierzchni prowadzi do przelewania się wody lub zbyt stromych skarp, które łatwo się osuwają. Zawsze warto pamiętać, żeby nie brać wymiarów „na oko”, tylko bazować na pewnych wzorach i przeliczyć sobie wszystko, zanim zaczniesz wykop. Z mojego doświadczenia powiem, że w praktyce terenowej warto zostawić nawet minimalny zapas, bo czasem skarpy mogą się obsunąć, jeśli podłoże jest grząskie. Branżowo zwraca się uwagę, by nachylenie skarp nie było zbyt strome, bo wtedy rów szybciej się niszczy i traci parametry użytkowe. Stąd właśnie takie szerokości – nie są przypadkowe, tylko wynikają z długoletnich doświadczeń i dobrych praktyk inżynierskich.