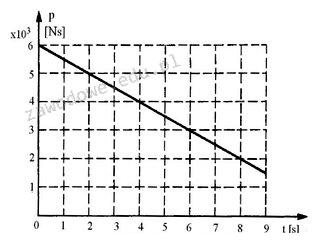
Poprawna odpowiedź to 4 razy, co wynika z zastosowania zasady dotyczącej energii kinetycznej, która jest bezpośrednio związana z pędem. Energia kinetyczna (Ek) samolotu jest opisana wzorem Ek = (p^2)/(2m), gdzie p to pęd, a m to masa. W analizowanej sytuacji, zmiana pędu z 5 x 10^3 Ns do 2.5 x 10^3 Ns pokazuje, że nowa wartość pędu jest połową pierwotnej. Zastosowując wzór na energię kinetyczną, możemy zauważyć, że jeśli pęd zmniejsza się o połowę, to energia kinetyczna zmniejsza się o czynnik (1/2)^2, co daje nam 1/4 pierwotnej wartości. Stąd wynika, że energia kinetyczna zmniejszyła się czterokrotnie. Takie obliczenia są istotne w kontekście inżynierii lotniczej, gdzie precyzyjne obliczenia energii i pędu są kluczowe dla oceny wydajności i bezpieczeństwa lotów. Wiedza ta jest również przydatna w symulacjach dynamicznych pojazdów, co jest standardem w projektowaniu i badaniach lotniczych.
Wybór którejkolwiek z pozostałych odpowiedzi prowadzi do błędnych wniosków na temat relacji między pędem a energią kinetyczną. Wiele osób może mylnie zakładać, że zmniejszenie pędu o 50% automatycznie przekłada się na proporcjonalne zmniejszenie energii kinetycznej, co jest fundamentalnym nieporozumieniem. Zgodnie z zasadą konstytucji energii, energia kinetyczna nie jest liniowo związana z pędem, ale jest funkcją kwadratową. Oznacza to, że nawet małe zmiany w pędzie mają znaczny wpływ na energię kinetyczną. Wybranie odpowiedzi wskazującej na mniejsze zmniejszenie energii, jak 2 razy czy 3 razy, sugeruje, że pomijane jest zrozumienie, iż energia kinetyczna jest proporcjonalna do kwadratu pędu. Takie błędne podejście do analizy może wynikać z braku doświadczenia w pracy z tymi pojęciami, co jest kluczowe w dziedzinach takich jak fizyka i inżynieria. W rzeczywistości zrozumienie tej relacji jest niezbędne do prawidłowego modelowania zjawisk dynamicznych i optymalizacji wydajności systemów mechanicznych. Dlatego w kontekście oceny energii i pędu, ważne jest, aby pamiętać o kwadratowym charakterze tej relacji, co pozwala uniknąć powszechnych błędów w analizie danych energetycznych.