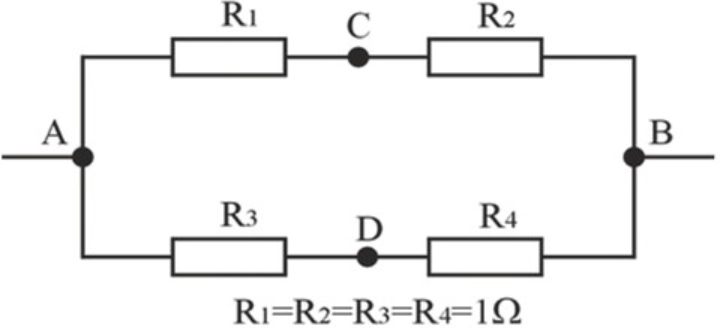
Zgadza się! Poprawna odpowiedź to 1 Ω. Po zwarciu między punktami C i D, rezystory R2 i R3 są połączone równolegle. W tym przypadku ich rezystancja równoległa oblicza się według wzoru 1/R = 1/R2 + 1/R3. Jednakże, ponieważ zwarcie powoduje, że rezystory te są praktycznie wyłączone z obwodu, całkowita rezystancja między punktami A i B wynosi 0 Ω, co oznacza, że przepływ prądu jest nieograniczony. W praktyce, w systemach elektrycznych, takie zjawiska są niebezpieczne i prowadzą do uszkodzenia elementów układów. W przypadku projektowania obwodów, kluczowe jest uwzględnienie potencjalnych zwarć, dostosowując dobór komponentów oraz stosując odpowiednie zabezpieczenia, takie jak bezpieczniki czy wyłączniki różnicowoprądowe, które zapobiegają skutkom zwarć i zapewniają bezpieczeństwo użytkowników.
Chociaż wybór 2 Ω może wydawać się logiczny, to jednak nie jest on poprawny w kontekście przedstawionego obwodu. Warto zwrócić uwagę na to, że po zwarciu między punktami C i D, rezystory R2 i R3 nie działają z równoległej konfiguracji, a ich wpływ na całkowitą rezystancję jest znikomy. W rzeczywistości zwarcie stwarza sytuację, w której przynajmniej jeden z obwodów staje się otwarty, co prowadzi do tego, że rezystancja na punktach A i B wynosi 0 Ω. W obwodach elektrycznych kluczowe jest zrozumienie, w jaki sposób różne elementy wpływają na siebie nawzajem. Wybór 4 Ω także sugeruje błędne myślenie, ponieważ nie uwzględnia faktu, że całkowita rezystancja w efekcie zwarcia powinna być znacznie niższa, a nie wyższa niż w normalnym stanie. Natomiast wybór 1 Ω może wynikać z nieprecyzyjnego obliczenia rezystancji równoległej, co jest częstym błędem w analizie obwodów. Dlatego ważne jest, aby przy rozwiązywaniu problemów z obwodami elektrycznymi, zawsze zwracać uwagę na układ i wartości poszczególnych elementów w kontekście ich połączeń oraz funkcji, jakie pełnią w danym obwodzie.