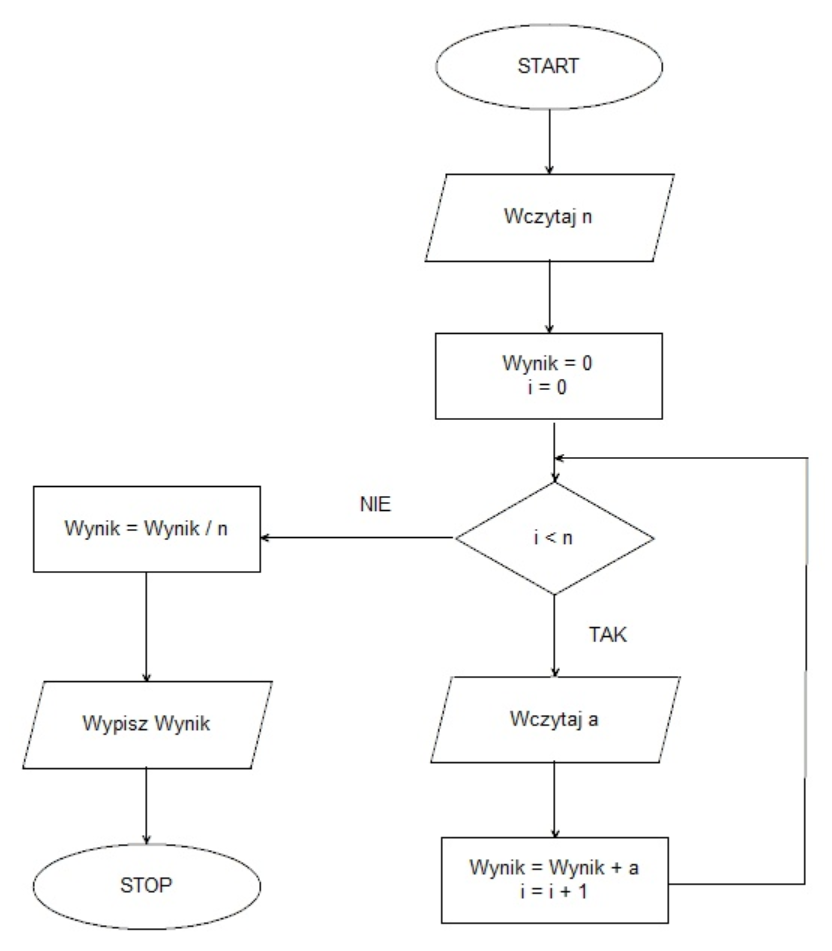
Algorytm z diagramu realizuje dokładnie klasyczny wzór na średnią arytmetyczną. Najpierw wczytywana jest liczba n – ile wartości użytkownik poda. Potem zmienna „Wynik” jest zerowana, a zmienna sterująca pętlą i ustawiana na 0. Następnie działa pętla z warunkiem i < n: w każdej iteracji program wczytuje kolejną liczbę a, dodaje ją do zmiennej Wynik (czyli de facto sumuje wszystkie podane liczby), a licznik i zwiększa o 1. Gdy i przestaje być mniejsze od n, pętla się kończy i dopiero wtedy wykonywana jest operacja Wynik = Wynik / n. To jest dokładnie to, co robi wzór: średnia = (a1 + a2 + … + an) / n. Z praktycznego punktu widzenia taki algorytm to absolutna podstawa w programowaniu, szczególnie przy pracy z danymi wejściowymi: wynikami pomiarów, ocenami uczniów, czasami odpowiedzi serwera itp. W wielu językach programowania (C, Java, JavaScript, PHP) napisanie tego w kodzie sprowadza się do jednej pętli for lub while, sumowania zmiennej i jednego dzielenia na końcu. Dobrą praktyką jest, żeby dzielenie wykonywać dopiero po zsumowaniu wszystkich elementów, dokładnie tak jak na diagramie, a nie w każdej iteracji, bo to ogranicza błędy zaokrągleń i jest po prostu wydajniejsze obliczeniowo. W aplikacjach webowych ten schemat pojawia się np. przy liczeniu średniej oceny produktu z wielu głosów użytkowników, średniego czasu odpowiedzi API albo średniego czasu spędzonego na stronie. Moim zdaniem to jedno z kluczowych ćwiczeń na zrozumienie pętli i zmiennych pomocniczych, bo łączy matematykę z bardzo praktyczną logiką algorytmiczną.
Na diagramie widać dość typowy schemat algorytmu: wczytanie n, zainicjowanie zmiennych, pętla z licznikiem i i na końcu pojedyncza operacja dzielenia. Taki układ często myli osoby początkujące, bo łatwo go skojarzyć z innymi pojęciami matematycznymi. Warto więc spokojnie prześledzić logikę. Najpierw ustalana jest liczba elementów n. Potem zmienna Wynik jest ustawiana na 0, a i na 0, więc mamy klasyczne przygotowanie do sumowania w pętli. Warunek i < n powoduje, że ciało pętli wykona się dokładnie n razy. W każdej iteracji wczytywana jest jedna liczba a, a następnie Wynik = Wynik + a. To jest zwykłe sumowanie wszystkich podanych wartości. Dopiero po wyjściu z pętli następuje pojedyncza operacja Wynik = Wynik / n. To wyklucza interpretację w stylu „reszta z dzielenia” lub „najmniejszy wspólny dzielnik”, bo w algorytmie nie ma ani operatora modulo, ani żadnej logiki opartej na dzielnikach, porównywaniu reszt, iteracyjnej redukcji NWD itp. Dla średniej geometrycznej potrzebne byłoby mnożenie wszystkich wartości, a na końcu pierwiastek n-tego stopnia. Tutaj nie ma ani mnożenia w pętli, ani pierwiastkowania, więc średnia geometryczna odpada. Typowym błędem myślowym jest patrzenie tylko na końcowe dzielenie przez n i dopowiadanie sobie różnych znaczeń: że to reszta, że to jakiś „wspólny dzielnik” albo inna bardziej skomplikowana operacja. Tymczasem według dobrych praktyk analizy algorytmów trzeba zawsze prześledzić pełny przebieg: co się dzieje z każdą zmienną w każdej iteracji pętli. Wtedy widać jasno, że algorytm realizuje sumę n wczytanych liczb i na końcu dzieli tę sumę przez n, czyli liczy zwykłą średnią arytmetyczną. W kontekście podstaw informatyki to klasyczny wzorzec: inicjalizacja, pętla z akumulacją, przetworzenie wyniku po zakończeniu pętli.