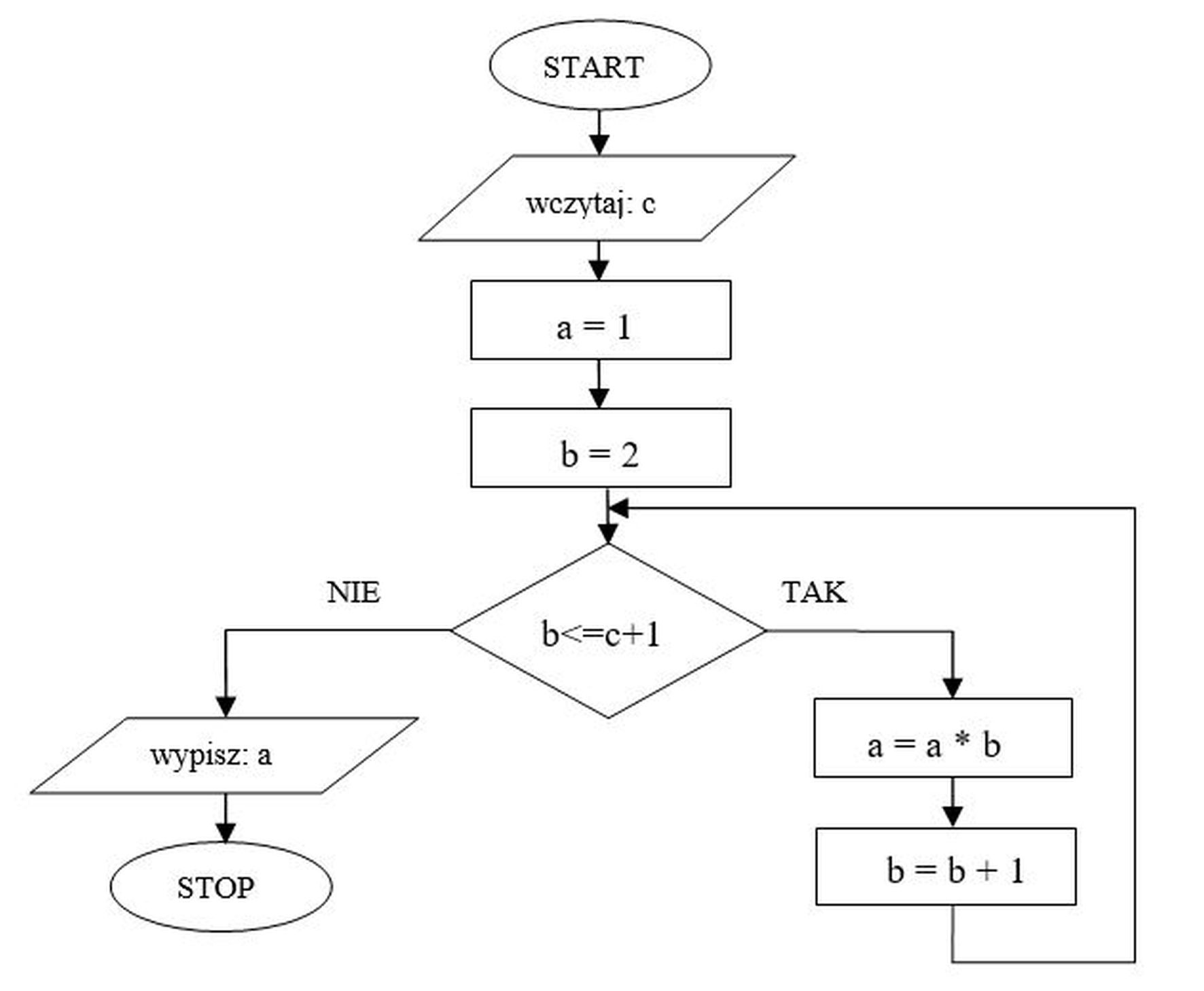
Poprawna odpowiedź 24 wynika z dokładnego prześledzenia działania algorytmu krok po kroku. Algorytm najpierw wczytuje wartość c, potem ustawia zmienne: a = 1 oraz b = 2. Następnie sprawdza warunek b <= c + 1. Dla c = 3 mamy c + 1 = 4, więc pętla działa tak długo, jak b <= 4. Teraz iteracje: 1) b = 2, 2 <= 4 – warunek spełniony, więc wykonujemy a = a * b, czyli a = 1 * 2 = 2, potem zwiększamy b: b = 3. 2) b = 3, 3 <= 4 – znowu TAK, więc a = 2 * 3 = 6, b zwiększa się do 4. 3) b = 4, 4 <= 4 – nadal TAK, więc a = 6 * 4 = 24, b rośnie do 5. 4) b = 5, 5 <= 4 – warunek już fałszywy, wychodzimy z pętli i wypisujemy a, czyli 24. W praktyce ten algorytm oblicza iloczyn kolejnych liczb naturalnych od 2 do c+1, czyli w tym przypadku 2 * 3 * 4. To jest po prostu część silni: 4! = 1 * 2 * 3 * 4, tylko bez początkowego 1, więc wynik jest taki sam. Warto tu zauważyć dobry nawyk: inicjacja zmiennej a wartością 1 jest klasycznym wzorcem przy obliczaniu iloczynów (neutralny element mnożenia). Tego typu konstrukcje pętli z warunkiem porównującym do c+1 pojawiają się bardzo często w programowaniu – zarówno w algorytmach obliczających silnię, jak i przy różnego rodzaju iteracjach po zakresach, np. w JavaScript czy PHP. Z mojego doświadczenia dobrze jest zawsze rozpisać sobie kolejne kroki na kartce, szczególnie gdy warunek zawiera dodawanie lub odejmowanie, bo to właśnie tam najłatwiej o pomyłkę o jeden krok (tzw. błąd off-by-one).
Żeby dobrze zrozumieć, dlaczego wyniki 6, 12 czy 60 nie są poprawne, trzeba spokojnie przeanalizować logikę całego schematu blokowego, a nie zatrzymywać się na pierwszym wrażeniu. Algorytm nie wykonuje pojedynczego mnożenia, tylko korzysta z pętli sterowanej zmienną b oraz warunkiem b <= c + 1. Takie konstrukcje są typowym źródłem pomyłek typu „o jeden za mało” lub „o jeden za dużo”, bo łatwo przeoczyć, że granica to właśnie c+1, a nie samo c. Częsta błędna intuicja jest taka: skoro c = 3, to b zaczyna od 2, więc mnożymy 1 * 2 * 3 i dostajemy 6. To wygląda logicznie, ale pomija fakt, że warunek dopuszcza jeszcze b = 4, bo sprawdzamy b <= 4, a nie b < 4. W efekcie pętla wykonuje się trzy razy: dla b = 2, 3 i 4. Stąd wynik 6 odpowiada jedynie sytuacji, gdyby warunek był zapisany jako b <= c (lub gdyby ktoś „w głowie” zakończył działanie pętli o jedną iterację za wcześnie). To klasyczny błąd przy ręcznej symulacji pętli. Podobnie wynik 12 zwykle bierze się z pomieszania kolejności operacji: ktoś policzy 2 * 3 = 6, potem doda 4 zamiast znowu pomnożyć, albo przerwie analizę po dwóch krokach. To pokazuje, jak ważne jest trzymanie się dosłownie instrukcji: a = a * b oznacza zawsze mnożenie, bez żadnych wyjątków. Z kolei 60 może być efektem całkowicie oderwanego od schematu zgadywania, albo próby „dopisywania” dodatkowych kroków, jakby pętla wykonywała się jeszcze dla kolejnych wartości, których warunek już nie dopuszcza. Z mojego doświadczenia warto przy takich zadaniach zawsze wypisać kolejne stany zmiennych a i b w tabelce: po inicjalizacji, po każdej iteracji i po wyjściu z pętli. To jest bardzo dobra praktyka, zgodna z profesjonalnym podejściem do analizy algorytmów, bo pozwala wyłapać wszystkie nieporozumienia związane z warunkiem końca pętli. Takie umiejętności przydają się potem w realnym kodzie, niezależnie czy piszesz w JavaScript, PHP, czy w innym języku – unikniesz wtedy typowych bugów związanych ze złym zakresem pętli i błędami obliczeń.