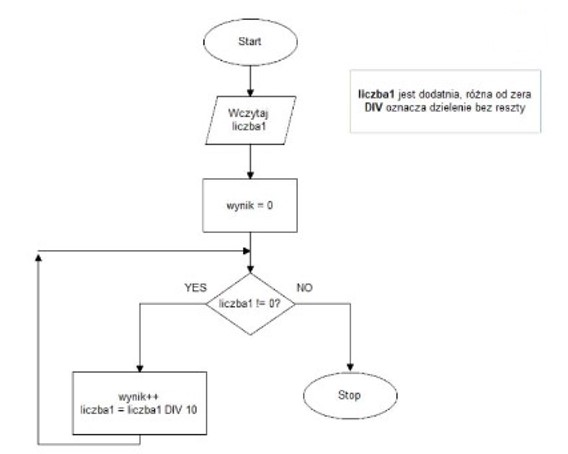
Wybierając odpowiedź dotyczącą liczby cyfr w wprowadzonej liczbie, pokazujesz dobre zrozumienie tego, jak działa prezentowany algorytm. W praktyce bardzo często spotyka się podobne rozwiązania, gdy trzeba np. zliczyć, ile znaków ma PESEL, numer telefonu lub numer identyfikacyjny w bazie danych. Algorytm wykonuje bardzo prostą, ale jednocześnie sprytną operację – dzieli podaną liczbę przez 10 (zawsze całkowicie, bez reszty), aż ta liczba się wyzeruje. Za każdym obrotem pętli zwiększa licznik, więc po zakończeniu działania licznik wskazuje, ile razy można było podzielić liczbę przez 10, czyli ile było w niej cyfr. To dokładnie odpowiada liczbie cyfr w zapisie dziesiętnym. Podejście to jest bardzo efektywne, bo nie wymaga konwersji liczby na tekst ani używania dodatkowych struktur danych. W profesjonalnym kodzie często preferuje się takie rozwiązania – są szybkie i niezawodne. Moim zdaniem warto znać ten wzorzec, bo przydaje się zarówno w algorytmice, jak i analizie danych czy podczas implementacji walidacji pól liczbowych w bazach danych lub formularzach. Dodatkowo, zgodnie z dobrymi praktykami, algorytm nie ulega błędom związanym z nietypowymi danymi – działa dla każdej dodatniej liczby całkowitej. Warto zapamiętać takie sztuczki, bo potem życie programisty jest łatwiejsze.
Analizując algorytm przedstawiony na schemacie, łatwo zauważyć, że nie wykonuje on ani sumowania cyfr, ani nie oblicza największego wspólnego dzielnika, ani nie sumuje wprowadzonych liczb. W praktyce mylenie tych operacji wynika często z pobieżnego czytania algorytmu lub automatycznego kojarzenia słowa „wynik” z sumą. Jednak podstawą analizy algorytmów zawsze powinno być zwracanie uwagi na konkretne instrukcje i sposób przetwarzania danych. W tym przypadku liczba jest dzielona przez 10 w każdej iteracji pętli, a licznik jest zwiększany o jeden za każdym razem, gdy to się dzieje. Nie ma tu żadnego dodawania poszczególnych cyfr, co wyklucza sumowanie cyfr. Nie pojawia się przetwarzanie wielu różnych liczb, więc niemożliwe jest sumowanie wprowadzonych liczb – algorytm pracuje wyłącznie na jednej wartości podanej na wejściu. Narzędzie do obliczania największego wspólnego dzielnika musiałoby operować na dwóch liczbach i wykorzystywać inne operacje, jak reszta z dzielenia. Typowym błędem jest też utożsamianie każdej pętli z operacją sumowania lub łączenia danych, co w tym przypadku nie ma uzasadnienia merytorycznego. Kluczowe jest przy analizie algorytmów zwracanie uwagi na to, jakie operacje są wykonywane w każdej iteracji i czy pojawia się obsługa wielu wartości, czy tylko jednej. Z mojego doświadczenia wynika, że takie drobne błędy myślowe prowadzą często do fałszywych wniosków, dlatego warto dokładnie czytać algorytm krok po kroku i analizować, do czego rzeczywiście prowadzą poszczególne instrukcje. W tym przypadku algorytm po prostu liczy liczbę dziesiętnych „pozycji” w liczbie aż do jej wyzerowania, co odpowiada liczbie cyfr, a nie żadnej z pozostałych interpretacji.