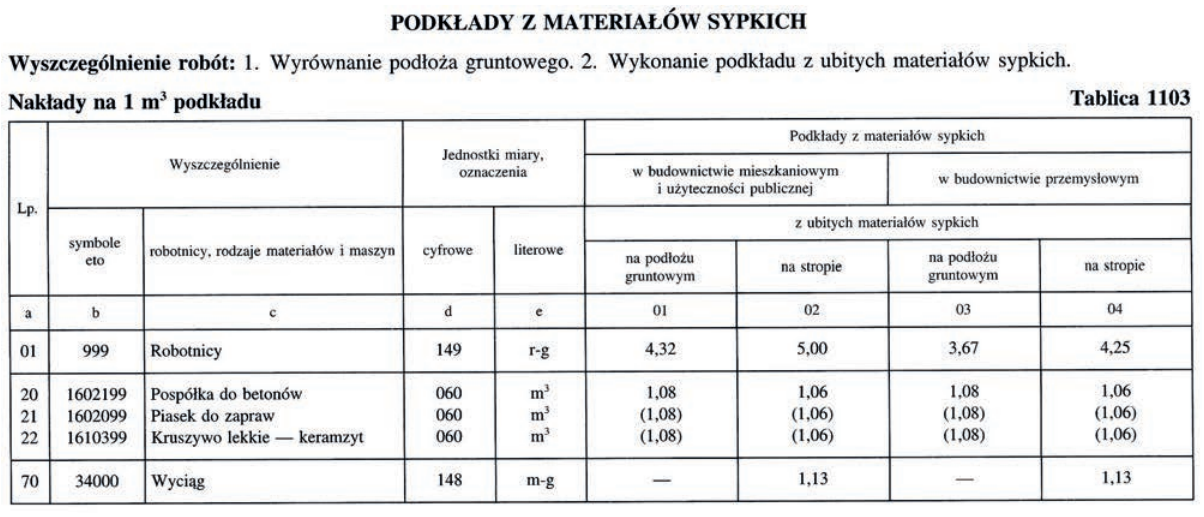
Obliczenie ilości zużytego piasku jest kluczowe w procesie budowlanym, a poprawna odpowiedź wynika z precyzyjnych obliczeń objętości. Zgodnie z danymi, powierzchnia podłoża wynosi 40 m2, a średnia grubość warstwy piasku to 0,20 m. Aby obliczyć objętość piasku, stosujemy wzór: V = A * h, gdzie V to objętość, A to powierzchnia, a h to wysokość. Po podstawieniu danych otrzymujemy V = 40 m2 * 0,20 m = 8 m3. Jednakże, piasek nie jest materiałem o stałej objętości po zagęszczeniu. W praktyce, stosuje się współczynnik zagęszczenia, który dla piasku wynosi 1,08. Dlatego całkowita ilość zużytego piasku wynosi V * 1,08 = 8 m3 * 1,08 = 8,64 m3. Takie obliczenia są zgodne z ogólnymi normami i dobrymi praktykami w budownictwie, które wymagają uwzględnienia zmian objętości materiałów budowlanych po ich aplikacji. Warto znać tę metodę, aby uniknąć niedoborów materiałowych lub nadwyżek, co może wpłynąć na budżet projektu.
Podejmując próbę obliczenia ilości zużytego piasku, istotnym jest zrozumienie podstawowych zasad związanych z objętością oraz zagęszczeniem materiałów. Odpowiedzi, które nie uwzględniają właściwego wzoru na obliczenie objętości podkładu, są nieprawidłowe. Na przykład, uzyskanie wartości 4,32 m3 sugeruje, że może być rozważany błędny współczynnik wysokości lub powierzchni. Z kolei odpowiedzi takie jak 3,67 m3 oraz 10,00 m3 mogą wynikać z błędnego zrozumienia, że objętość materiału można obliczyć bez uwzględnienia właściwego współczynnika zagęszczenia. Często popełnianym błędem jest używanie nieprawidłowych danych wejściowych, takich jak niewłaściwa grubość warstwy lub powierzchnia, co prowadzi do znacznych rozbieżności w obliczeniach. Dodatkowo, niektórzy mogą pomijać istotny parametr, jakim jest współczynnik zagęszczenia, który jest kluczowy w przypadku materiałów sypkich. Należy pamiętać, że w praktyce budowlanej zaniedbanie tego aspektu może prowadzić do poważnych problemów, takich jak nierównomierne osiadanie podłoża, co negatywnie wpłynie na stabilność konstrukcji. Dlatego właściwe zrozumienie zastosowania odpowiednich wzorów oraz uwzględnienie wszystkich istotnych parametrów jest kluczowe dla uzyskania precyzyjnych wyników w obliczeniach inżynieryjnych.