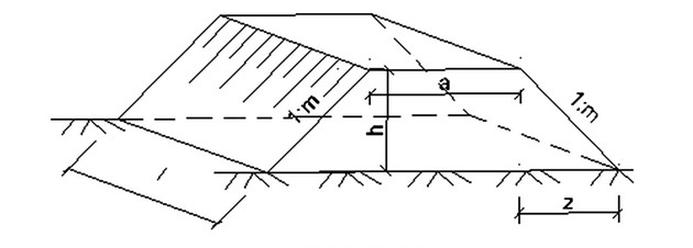
Poprawna odpowiedź to 3600 m3, co wynika z właściwego obliczenia objętości nasypu. Aby obliczyć objętość graniastosłupa, należy najpierw określić pole podstawy, którym w tym przypadku jest trapez. Podstawy trapezu to długość a oraz długość b, którą możemy wyznaczyć na podstawie podanych wymiarów. Wysokość trapezu z, oraz jego długość h są kluczowe do obliczeń. Po obliczeniu pola trapezu, otrzymujemy wartość, którą następnie mnożymy przez długość nasypu l, co daje nam ostateczną objętość. W praktyce obliczenia takie są niezbędne w geotechnice i budownictwie, gdzie precyzyjne określenie objętości materiałów sypkich jest kluczowe dla kosztorysowania oraz planowania prac budowlanych. Warto znać także metody weryfikacji obliczeń, takie jak obliczenia przy użyciu oprogramowania inżynieryjnego, które mogą znacząco ułatwić pracę inżyniera.
Wybierając jedną z niepoprawnych odpowiedzi, można zauważyć typowe nieporozumienia związane z obliczeniami objętości. Na przykład, odpowiedzi takie jak 1800 m2 i 3600 m2 są wynikiem pomylenia jednostek miary, gdzie powierzchnia mylnie została zinterpretowana jako objętość. W przypadku objętości zawsze musimy pracować w jednostkach sześciennych, natomiast metry kwadratowe odnoszą się do powierzchni, co nie ma zastosowania w obliczeniach dotyczących objętości. Z kolei odpowiedź 1800 m3 może wynikać z błędnych założeń dotyczących wymiarów podstawy trapezu i niewłaściwego obliczenia pola. Często błędy te pojawiają się, gdy nie uwzględnia się wszystkich wymiarów lub nieprawidłowo interpretuje się geometrę obiektu. Kluczowym elementem w takich obliczeniach jest dokładność oraz znajomość wzorów matematycznych, co jest niezbędne, aby uniknąć takich pułapek. W praktyce, szczegółowe zrozumienie koncepcji geometrii przestrzennej i umiejętności poprawnego stosowania wzorów na pola i objętości są niezwykle istotne w codziennej pracy inżynierów budowlanych oraz specjalistów zajmujących się projektowaniem i realizacją robót ziemnych.