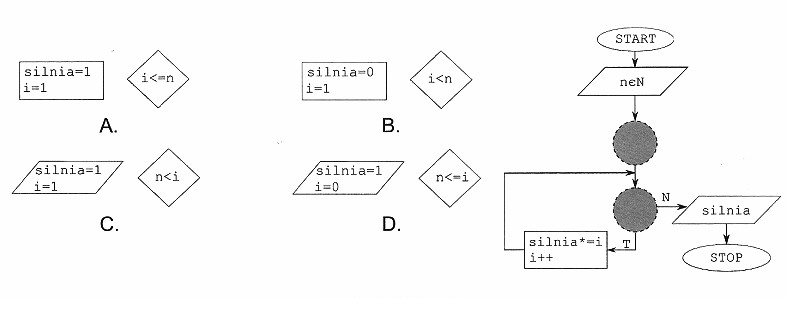
Odpowiedź A jest poprawna, ponieważ algorytm obliczania silni rozpoczyna swoje działanie od zainicjowania zmiennej 'silnia' na wartość 1. Jest to kluczowy krok, ponieważ silnia z liczby 0 (0!) jest zdefiniowana jako 1, co stanowi podstawę dla dalszych obliczeń. W każdym kroku pętli algorytm mnoży aktualną wartość silni przez kolejne liczby naturalne, co zgodne jest z definicją silni, która mówi, że n! = n × (n-1)!. Taki proces umożliwia poprawne obliczenie wartości silni dla dowolnej liczby naturalnej n, przy założeniu, że liczba ta jest nieujemna. W praktyce, obliczanie silni znajduje zastosowanie w różnych dziedzinach, od kombinatoryki po rachunek różniczkowy. Na przykład, silnia odgrywa kluczową rolę w obliczeniach prawdopodobieństwa, przy permutacjach i kombinacjach. Użycie odpowiednich bloków w algorytmie oraz jego poprawna konstrukcja są zgodne z najlepszymi praktykami w programowaniu, co zapewnia nie tylko efektywność, ale także czytelność i łatwość w utrzymaniu kodu.
Wybór niepoprawnej odpowiedzi może wynikać z niepełnego zrozumienia zasad działania algorytmu obliczania silni. Kluczowym elementem jest zainicjowanie zmiennej, która będzie przechowywać wynik obliczeń. W przypadku, gdy wartość ta nie została by poprawnie ustawiona na 1, algorytm nie byłby w stanie obliczyć silni poprawnie. Istnieje kilka powszechnych błędów myślowych, które mogą prowadzić do takich niepoprawnych odpowiedzi. Przykładem jest założenie, że silnia powinna być początkowo równa 0, co jest nieprawidłowe, ponieważ 0! = 1. Innym częstym błędem jest pominięcie kluczowego kroku mnożenia przez liczby naturalne, co prowadziłoby do braku postępu w obliczeniach i błędnych wyników. W praktyce, błędy w algorytmach, takie jak pominięcie inicjalizacji lub niewłaściwe operacje w pętli, mogą skutkować nieskończonymi pętlami lub niepoprawnymi wynikami, co jest niepożądane w programowaniu. Dobrą praktyką jest stosowanie standardów kodowania, które zapewniają jasność i poprawność algorytmów, a także testowanie kodu w różnych scenariuszach, aby upewnić się, że działa on zgodnie z oczekiwaniami.