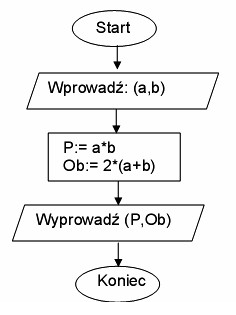
Poprawna odpowiedź to blok wejścia-wyjścia, ponieważ w kontekście diagramów blokowych, blok ten jest odpowiedzialny za wprowadzanie danych do programu i wyprowadzanie wyników. W przypadku obliczania pola i obwodu prostokąta, wyniki są prezentowane w bloku oznaczonym jako 'Wyprowadź (P, Ob)', co jest klasycznym przykładem użycia bloku wejścia-wyjścia. Tego rodzaju bloki są powszechnie stosowane w programowaniu oraz inżynierii systemowej do modelowania wymiany danych pomiędzy różnymi komponentami systemu. Dobre praktyki w tym obszarze sugerują, aby wyraźnie oddzielać logikę obliczeniową od operacji wejścia-wyjścia, co zwiększa czytelność i ułatwia późniejsze modyfikacje. W praktyce zastosowanie bloków wejścia-wyjścia jest kluczowe podczas projektowania systemów, takich jak aplikacje obliczeniowe, gdzie wyniki muszą być dostępne dla użytkownika końcowego bądź innych modułów systemu.
Wybór odpowiedzi spośród opcji warunkowych, operacyjnych lub zakończenia sugeruje niepełne zrozumienie funkcji poszczególnych bloków w diagramach blokowych. Blok warunkowy jest używany do podejmowania decyzji w programie, co oznacza, że jego działanie jest ściśle związane z warunkami logicznymi. Na przykład, blok ten może decydować, czy kontynuować obliczenia na podstawie spełnienia określonego kryterium. Odpowiedź operacyjna odwołuje się do bloków, które wykonują konkretne operacje na danych, takie jak dodawanie czy mnożenie. Z kolei blok zakończenia jest używany do sygnalizowania końca procesu obliczeniowego, co nie jest związane z wyprowadzaniem wyników dla użytkownika. Mylne zrozumienie tych terminów może prowadzić do nieprawidłowych wniosków dotyczących funkcji bloków w schematach. W kontekście obliczeń, wynik pola i obwodu prostokąta musi być skutecznie wyprowadzony na zewnątrz programu, co intuicyjnie wskazuje na zastosowanie bloku wejścia-wyjścia. Typowym błędem w myśleniu jest utożsamianie wszystkich bloków z jedną funkcją, co prowadzi do zniekształcenia rzeczywistego funkcjonowania diagramów blokowych i ich roli w logice programowania. Zrozumienie tych różnic jest kluczowe dla efektywnego tworzenia diagramów, które prawidłowo przedstawiają procesy logiczne w programowaniu.