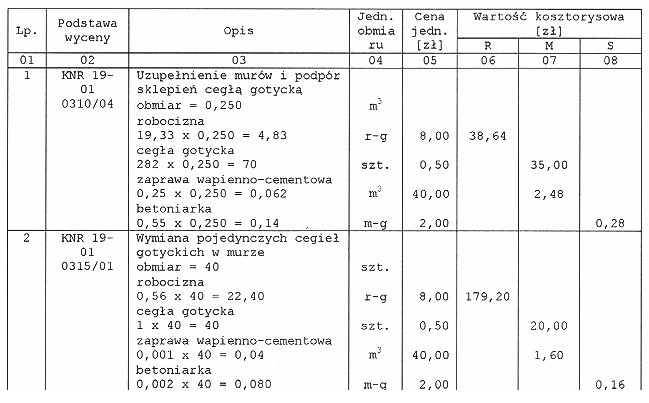
Poprawna odpowiedź wynika z poprawnego zastosowania zasad obliczania wartości kosztorysowej. Aby określić koszt cegieł gotyckich, należy pomnożyć ilość potrzebnych cegieł przez ich cenę jednostkową. W analizowanym fragmencie kosztorysu wskazano, że potrzeba 40 sztuk cegieł, a cena jednostkowa wynosi 0,50 zł za sztukę. W związku z tym, obliczenia przedstawiają się następująco: 40 sztuk x 0,50 zł = 20,00 zł. Obliczanie wartości kosztorysowej jest kluczowe w zarządzaniu projektami budowlanymi, ponieważ pozwala dokładnie oszacować koszty oraz budżetować prace. Zrozumienie tych zasad jest istotne, aby uniknąć niedoszacowań lub przeszacowań, co może prowadzić do nieefektywnego zarządzania finansami projektu. W praktyce, warto również rozważyć zmiany cen materiałów oraz ich dostępność na rynku, co może wpłynąć na ostateczną wartość kosztorysową. Standardy kosztorysowania, takie jak normy PN-ISO 12006, podkreślają znaczenie precyzyjnych obliczeń oraz dokumentacji w procesie planowania i realizacji inwestycji budowlanych.
Wybór innych wartości niż 20,00 zł wskazuje na niezrozumienie podstawowych zasad kalkulacji kosztów w kontekście kosztorysowania. Często występującym błędem jest nieuwzględnienie poprawnego mnożenia ilości cegieł przez ich cenę jednostkową, co prowadzi do nieprawidłowych wyników. Na przykład, odpowiedzi takie jak 0,50 zł czy 40,00 zł mogą wynikać z nieprawidłowego odczytu danych z fragmentu kosztorysu lub błędnej interpretacji jednostek. Możliwe, że pojawia się mylne przekonanie, że 0,50 zł to całkowity koszt, a nie cena jednostkowa, co jest kluczowe w obliczeniach. W przypadku wskazania wartości 35,00 zł, można zauważyć, że jest to również wynik błędnego mnożenia – użytkownik mógł pomylić ilość cegieł z ich ceną, co jest typowym błędem w analizie kosztorysowej. Zrozumienie, że prawidłowe podejście polega na dokładnym przeliczeniu kosztów w oparciu o dostępne dane, jest niezbędne dla efektywnego zarządzania projektami budowlanymi. Warto również zwrócić uwagę na standardy kosztorysowania, które podkreślają znaczenie precyzyjnych obliczeń oraz ich dokumentacji, by uniknąć nieporozumień i błędów w przyszłości.