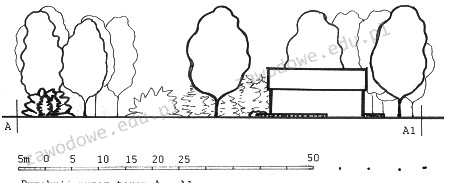
Odpowiedź 1:500 jest poprawna, ponieważ precyzyjnie odzwierciedla relację pomiędzy długością na rysunku a rzeczywistą długością w terenie. W przypadku skali liniowej, zauważamy, że 1 cm na rysunku odpowiada 5 m w rzeczywistości. Przemieniając metry na centymetry, uzyskujemy 5 m = 500 cm. Skala liczbowa jest wyrażona jako stosunek długości na rysunku do długości rzeczywistej. Dlatego, dla jednego centymetra na rysunku, mamy pięćset centymetrów w rzeczywistości, co daje nam 1:500. Takie podejście jest zgodne z powszechnie przyjętymi standardami w kartografii i geodezji, gdzie precyzyjne określenie skali jest kluczowe dla interpretacji map i planów, co jest niezbędne w pracach projektowych, planowaniu przestrzennym oraz inżynieryjnym. Użycie tego typu skali pozwala na właściwe oszacowanie odległości i powierzchni, co ma fundamentalne znaczenie dla projektów budowlanych, urbanistycznych oraz przy opracowywaniu dokumentacji technicznej.
Wybór innej odpowiedzi niż 1:500 wskazuje na pewne nieporozumienia dotyczące koncepcji skal i ich zastosowań. Odpowiedzi takie jak 1:5000, 1:50 czy 1:5 są oparte na błędnych założeniach co do relacji pomiędzy długością na rysunku a rzeczywistą. Na przykład, wybór skali 1:5000 oznaczałby, że 1 cm na rysunku odpowiada 50 m w rzeczywistości, co jest nieadekwatne do przedstawionych danych. Przy takim założeniu, 1 cm w rzeczywistości to 5000 cm, co jest znacznie większą odległością niż 5 m, a tym samym prowadzi do błędnych wniosków. Z kolei wybór skali 1:50 sugeruje, że 1 cm na rysunku to tylko 0,5 m w rzeczywistości, co również jest w sprzeczności z danymi. Ostatni przykład, 1:5, jest jeszcze bardziej mylący, ponieważ sugeruje, że rzeczywista odległość jest znacznie mniejsza niż na rysunku, co prowadziłoby do poważnych nieporozumień w kontekście rzeczywistych pomiarów. Te błędne interpretacje mogą wynikać z nieprecyzyjnego zrozumienia, jak działają skale i jak przekładają się na rzeczywiste wymiary. Dlatego ważne jest, aby przy analizie skal zawsze odnosić się do rzeczywistych konwersji jednostek oraz bazować na rzetelnych danych, co jest kluczowe w pracach związanych z geodezją i kartografią.