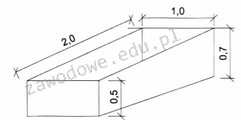
Odpowiedź 1,2 m3 jest poprawna, ponieważ objętość prostopadłościanu obliczamy jako iloczyn jego trzech wymiarów: długości, szerokości i wysokości. W tym przypadku mamy do czynienia z wymiarami 2,0 m, 1,0 m oraz wysokością użyteczną, którą należy obliczyć, odejmując grubość ściany od całkowitej wysokości. Z danych wynika, że całkowita wysokość to 0,7 m, a grubość ściany wynosi 0,1 m, co daje wysokość użyteczną równą 0,6 m. Mnożąc te wymiary (2,0 m * 1,0 m * 0,6 m), otrzymujemy objętość wykopu równą 1,2 m3. Obliczanie objętości jest kluczową umiejętnością w inżynierii budowlanej i architekturze, ponieważ pozwala na oszacowanie ilości materiałów potrzebnych do wykonania prac budowlanych, a także na planowanie przestrzenne. Umiejętność ta jest również niezbędna w kontekście zarządzania odpadami budowlanymi i efektywnego gospodarowania przestrzenią. W praktyce, znajomość zasad obliczania objętości pozwala na optymalne wykorzystanie zasobów i minimalizację kosztów budowy.
Wybór innej odpowiedzi może wynikać z kilku typowych nieporozumień dotyczących obliczeń objętości. Jednym z najczęstszych błędów jest nieprawidłowe uwzględnienie wysokości użytecznej wykopu. Nie można zapominać, że grubość ściany wpływa na rzeczywistą wysokość, którą należy uwzględnić w obliczeniach. Na przykład, jeżeli ktoś przyjmuje całkowitą wysokość bez uwzględnienia grubości ściany, prowadzi to do znacznie zawyżonych wartości objętości, co może skutkować błędnymi założeniami projektowymi oraz nieprawidłowym oszacowaniem kosztów. Kolejnym problemem może być mylenie jednostek miary lub błędne przeliczanie wymiarów, co jest szczególnie istotne w praktyce budowlanej, gdzie precyzja ma kluczowe znaczenie. Nieprawidłowe obliczenia mogą prowadzić do nadmiernych wydatków na materiały, a także do opóźnień w realizacji projektu. Warto pamiętać, że w inżynierii stosuje się różne standardy obliczeń, które mają na celu zachowanie wysokiej jakości i bezpieczeństwa projektów. Zrozumienie prawidłowego procesu obliczania objętości jest zatem nie tylko istotne dla uzyskania poprawnej odpowiedzi, ale również kluczowe dla sukcesu w praktycznych zastosowaniach inżynieryjnych.