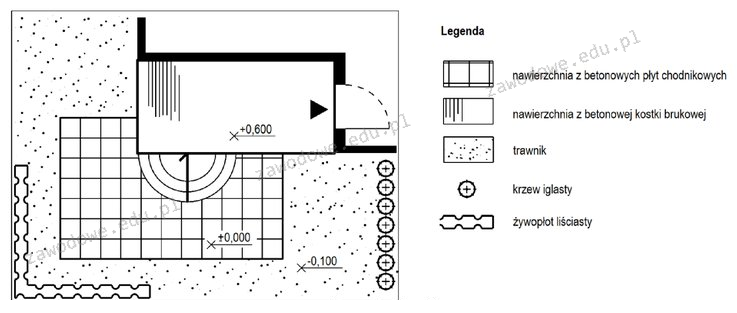
Poprawna odpowiedź to 0,7 m, co wynika z analizy poziomów na planie zagospodarowania ogrodu. Poziom tarasu z betonowej kostki brukowej wynosi +0,600 m, podczas gdy poziom trawnika to -0,100 m. Aby obliczyć różnicę wysokości pomiędzy tymi dwoma poziomami, należy zastosować prostą operację matematyczną: 0,600 - (-0,100), co równoważy się 0,600 + 0,100 = 0,700 m. Tego rodzaju obliczenia są kluczowe w planowaniu przestrzennym oraz w architekturze krajobrazu, ponieważ pozwalają na zrozumienie, jak różnice wysokości mogą wpłynąć na projekty budowlane i ich funkcjonalność. W praktyce znajomość różnic wysokości jest niezbędna, aby zapewnić odpowiednie odwodnienie terenu, zapobiec erozji oraz poprawić estetykę przestrzeni. Przykładem mogą być także tereny rekreacyjne, gdzie różnice wysokości mogą być wykorzystane do tworzenia naturalnych tarasów, które poprawiają komfort użytkowników oraz ułatwiają dostęp do różnych stref ogrodu.
Wybór innej odpowiedzi niż 0,7 m może wynikać z nieporozumień dotyczących interpretacji poziomów na planie zagospodarowania ogrodu. Często mylone są pojęcia poziomu terenu z poziomem konstrukcji. Na przykład, odpowiedzi takie jak 0,1 m, 0,5 m lub 0,6 m mogą być wynikiem błędnego odejmowania lub mylenia wartości dodatnich i ujemnych. Istotne jest, aby pamiętać, że przy obliczaniu różnic wysokości, te wartości muszą być traktowane z uwzględnieniem ich znaków. W przypadku poziomu tarasu, który jest dodatni (+0,600 m), i poziomu trawnika, który jest ujemny (-0,100 m), oznacza to, że różnica ta nie może być mniejsza od 0,6 m. Często zdarza się, że studenci przyjmują założenie, że różnice wysokości są mniejsze, gdyż nieprawidłowo interpretują znaki. Właściwe podejście wymaga przekształcenia wartości ujemnej w dodatnią podczas obliczeń, co jest kluczowe w kontekście architektury krajobrazu oraz budownictwa. Zrozumienie, jak różnice te wpływają na projekt i jego użytkowanie, jest fundamentalne dla uzyskania optymalnych rezultatów w zagospodarowaniu przestrzeni. Warto zatem przywiązywać dużą wagę do detali i dokładności w takich obliczeniach.