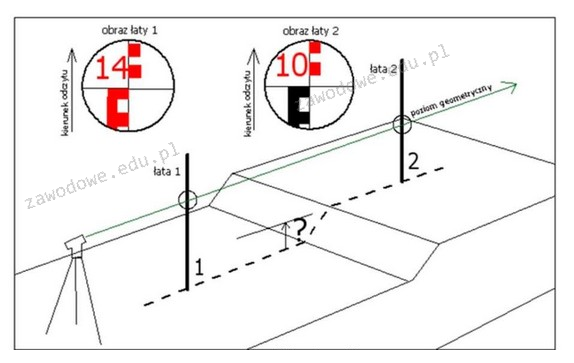
Różnica wysokości Δh<sub>1-2</sub> pomiędzy punktami 1 i 2 wynosi 4 dm, co jest wynikiem dokładnych pomiarów odczytów z łaty niwelacyjnej. W praktyce, aby obliczyć różnicę wysokości, należy zawsze odjąć odczyt z niższego punktu od odczytu z wyższego. W tym przypadku odczyty wynosiły 1,4 m dla punktu 1 i 1,0 m dla punktu 2. Odjęcie 1,0 m od 1,4 m daje 0,4 m, co po przeliczeniu daje 4 decymetry. Tego rodzaju pomiary są kluczowe w budownictwie oraz geodezji, gdzie precyzyjne określenie różnic wysokości jest podstawą dla dalszych prac, takich jak projektowanie konstrukcji czy prace ziemne. Warto pamiętać, że zgodnie z normami branżowymi, pomiary powinny być wykonywane z zachowaniem odpowiednich technik oraz przy użyciu dokładnych narzędzi, aby uniknąć błędów w obliczeniach oraz zapewnić wiarygodność wyników.
Często w pomiarach różnicy wysokości pojawiają się błędne założenia, które prowadzą do niewłaściwych odpowiedzi. W przypadku tego pytania, odpowiedzi 4 cm, 4 m oraz 4 mm są niepoprawne z kilku powodów. Przy analizie pomiarów niwelacyjnych kluczowe jest zrozumienie, że jednostki muszą być odpowiednio przeliczone oraz interpretowane. Odpowiedź 4 cm sugeruje, że różnica wysokości jest zbyt mała w kontekście podanych odczytów z łaty. Dla pomiarów w geodezji oraz budownictwie, różnice wysokości rzędu centymetrów mogą występować, ale w tym przypadku są one nieadekwatne do uzyskanych wartości. Odpowiedź 4 m natomiast jest nadmiernie zawyżona i wskazuje na fundamentalne nieporozumienie w interpretacji odczytów. Ostatecznie wartość 4 mm to również zbyt mała różnica, co prowadzi do konkluzji, że pomiar został źle przeprowadzony lub zinterpretowany. W praktyce ważne jest, aby przy pomiarze różnicy wysokości zawsze zwracać uwagę na pełne wartości w metrach i decymetrach, a także dbać o poprawność jednostek, co jest zgodne z zaleceniami standardów pomiarowych w geodezji. Dlatego kluczowe jest dokładne zrozumienie metodyki pomiarów oraz zastosowanie odpowiednich narzędzi, aby uzyskać precyzyjne i wiarygodne wyniki.