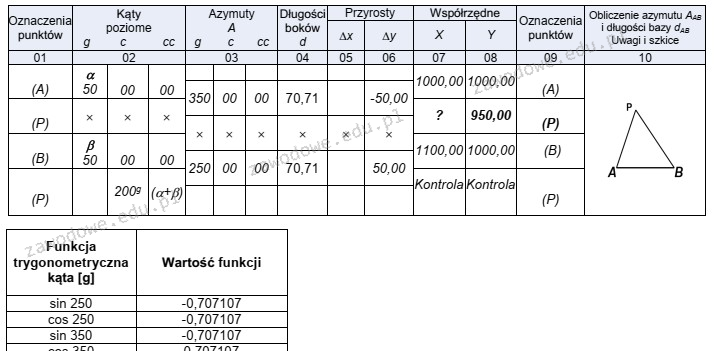
Poprawna odpowiedź to XP = 1050,00 m, co wynika z precyzyjnych obliczeń opartych na analizie współrzędnych w kontekście zmian ΔX. Obliczenia te polegają na zsumowaniu współrzędnej punktu A z różnicą ΔX, która została wyznaczona na podstawie danych z tabeli. W przypadku geodezji i inżynierii lądowej, bardzo ważne jest, aby dokładnie śledzić zmiany współrzędnych, co wpływa na dokładność pomiarów i późniejszych analiz. Praktycznie, takie obliczenia pozwalają na precyzyjne określenie lokalizacji punktu w przestrzeni, co jest kluczowe w wielu aplikacjach, takich jak projektowanie infrastruktury, nawigacja oraz w geodezyjnych rozliczeniach. Zrozumienie tego procesu jest fundamentem w pracy geodety, gdzie nie tylko trzeba umieć przeprowadzić obliczenia, ale też zrozumieć ich znaczenie w kontekście całego projektu. Analizując dane, należy zawsze brać pod uwagę potencjalne błędy pomiarowe oraz stosować odpowiednie metody korekcji, aby uzyskać jak najdokładniejsze wyniki.
Wybór niewłaściwej odpowiedzi może wynikać z kilku typowych błędów myślowych związanych z obliczeniami współrzędnych. Często przyczyną błędnych wyników jest nieprawidłowe zrozumienie, jak obliczać zmiany współrzędnych między punktami. Najczęściej zdarza się, że osoby podejmujące się takich obliczeń koncentrują się na pojedynczych wartościach, zamiast na całkowitym zestawieniu danych, co prowadzi do ograniczonej analizy sytuacji. Błędy mogą również wynikać z nieodpowiedniego uwzględnienia zmienności ΔX, co w kontekście pomiarów geodezyjnych jest kluczowe. Niezrozumienie tego, jak poszczególne zmiany wpływają na całkowity wynik, może prowadzić do pomyłek. Ponadto, niedostateczne znanie funkcji trygonometrycznych i ich zastosowań w obliczeniach kątowych może skutkować błędnymi wnioskami na temat wartości współrzędnych. Ważne jest, aby przy nauce geodezji i inżynierii lądowej wykorzystywać odpowiednie standardy oraz dobre praktyki, które pomagają w poprawnym przeprowadzaniu pomiarów i obliczeń. Aby uniknąć tych błędów, warto regularnie ćwiczyć obliczenia oraz brać pod uwagę całość kontekstu zagadnienia, a także korzystać z narzędzi i metod, które wspierają dokładność procesów pomiarowych.