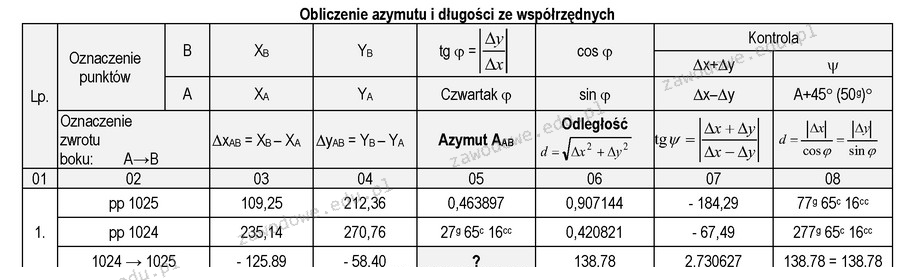
Obliczenie azymutu AAB w kontekście podanego fragmentu dziennika wymaga precyzyjnego podejścia do analizy współrzędnych. W pierwszej kolejności, kluczowe jest zrozumienie, że różnice współrzędnych ΔXAB i ΔYAB pomagają określić lokalizację punktu B względem punktu A. W tym przypadku, oba przyrosty są ujemne, co oznacza, że punkt B znajduje się w trzeciej ćwiartce układu współrzędnych. W takiej sytuacji, aby obliczyć azymut, dodajemy 200g do obliczonego kąta φ. Taki sposób obliczeń jest zgodny z ogólnie przyjętymi praktykami w geodezji oraz nawigacji. Praktyczne zastosowanie tej wiedzy jest nieocenione w różnych dziedzinach, takich jak inżynieria lądowa, geologia czy projektowanie systemów nawigacyjnych, gdzie precyzyjne obliczenia azymutu są kluczowe dla prawidłowego określenia kierunku i lokalizacji obiektów. Warto również zauważyć, że umiejętność obliczania azymutów i interpretacji wyników jest istotną kompetencją, która przydaje się w pracy z systemami GIS oraz w terenowych pomiarach geodezyjnych.
Obliczenia azymutu wymagają dokładności oraz zrozumienia układu współrzędnych, co jest szczególnie ważne w praktykach geodezyjnych i inżynieryjnych. W przypadku błędnych odpowiedzi, wiele osób może pomylić się w obliczeniach różnic współrzędnych, co prowadzi do niewłaściwego określenia lokalizacji punktu B. Na przykład, w sytuacji, gdy przyrosty współrzędnych są ujemne, kluczowe jest prawidłowe zinterpretowanie ich wpływu na położenie punktu w trzeciej ćwiartce układu. Nieprawidłowe dodanie 200g do kąta φ, lub jego pominięcie, może skutkować znacznymi błędami w obliczonej wartości azymutu. Często popełnianym błędem jest także nieprawidłowe przyjęcie wartości kątów w poszczególnych ćwiartkach, co prowadzi do dalszych dezinformacji. W obliczeniach geodezyjnych uznaje się standardy, które wymagają precyzyjnego podejścia do pomiarów i obliczeń, a stosowanie błędnych wzorów lub metod obliczeniowych może prowadzić do błędów w projekcie czy analizie terenowej. Warto zwrócić uwagę, że doświadczenie i praktyka są kluczowe, aby unikać typowych pułapek w obliczeniach azymutów, co podkreśla znaczenie nauki z błędów oraz ciągłego doskonalenia umiejętności w obszarze geodezji.