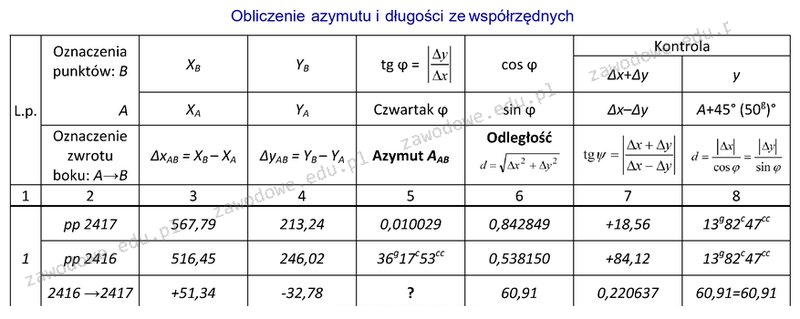
Poprawna odpowiedź to 363g82c47cc, ponieważ obliczenia dotyczące azymutu kierunku pp 2416 → pp 2417 zostały przeprowadzone zgodnie z odpowiednimi wzorami i zasadami geodezyjnymi. Kluczowym krokiem jest obliczenie tangensa kąta φ, który uzyskujemy z różnic wartości y i x. W przypadku naszych danych Δy wynosi -32,78, a Δx 51,34, co daje tg φ = Δy/Δx = -32,78 / 51,34 = -0,638293. Używając funkcji odwrotnej tangensa, obliczamy φ = arctg(-0,638293) = -32°32'13". Następnie, aby otrzymać azymut, dodajemy 360° do obliczonego kąta, ponieważ Δx jest dodatnie, a Δy ujemne, co wskazuje na położenie w II ćwiartce układu współrzędnych. Tak więc, azymut wynosi 360° + (-32°32'13") = 327°27'47". Przeliczając na format gradowy, uzyskujemy 363,8247g, co zaokrągla się do 363g82c47cc. W praktyce, znajomość obliczania azymutów ma kluczowe znaczenie w geodezji oraz nawigacji, gdzie precyzyjne wytyczenie kierunków jest niezbędne w pracach terenowych oraz podczas projektowania infrastruktury.
Aby zrozumieć, dlaczego odpowiedzi inne niż 363g82c47cc są nieprawidłowe, warto zwrócić uwagę na kilka kluczowych aspektów związanych z obliczaniem azymutów. Wiele z błędnych odpowiedzi może wynikać z nieprawidłowego zastosowania wzorów do obliczeń, zwłaszcza w kontekście zmiany znaku podczas przechodzenia przez ćwiartki układu współrzędnych. Na przykład, niektórzy mogą błędnie zakładać, że azymut można uzyskać bez uwzględnienia położenia punktów w układzie, co prowadzi do pomyłek w określaniu kąta. Często zdarza się także, że użytkownicy nie przeliczą prawidłowo wartości kątów z systemu stopniowego na system gradowy, co skutkuje dalszymi nieprawidłowościami. Na przykład, jeśli ktoś obliczy φ jako pozytywny, może uzyskać wartość azymutu, która nie odpowiada rzeczywistej lokalizacji punktów. Warto również zauważyć, że zastosowanie funkcji odwrotnej tangensa wymaga uwzględnienia kwadrantów, w których się znajdujemy, co jest kluczowe dla uzyskania prawidłowego wyniku. Błędy w interpretacji danych, takie jak pomyłki w różnicach Δy i Δx, mogą prowadzić do całkowicie błędnych wartości, które nie mają zastosowania praktycznego w geodezji czy nawigacji. Dlatego przy obliczeniach zawsze należy zwracać uwagę na detale i stosować się do standardów branżowych, aby zapewnić dokładność i niezawodność wyników.