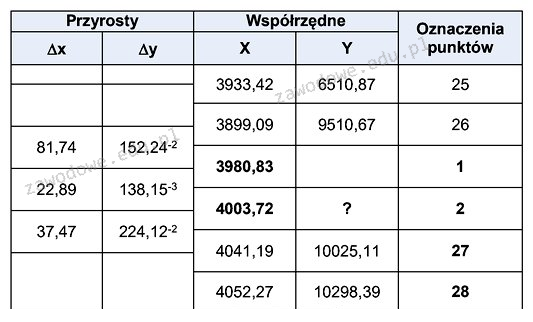
Obliczenie wartości współrzędnej Y punktu 2 w dwustronnym ciągu poligonowym polega na prawidłowym dodaniu przyrostu Δy do współrzędnej Y punktu 1. Współrzędna Y punktu 1 wynosi 9510,67 m, a przyrost Δy między punktami 1 i 2 wynosi 0,13815 m. Po wykonaniu operacji dodawania otrzymujemy wartość 9510,80815 m. Po zaokrągleniu do dwóch miejsc po przecinku, uzyskujemy 9510,81 m. Takie obliczenia są zgodne z metodologią prowadzoną w geodezji, gdzie dokładność pomiarów i obliczeń jest kluczowa. W praktyce, precyzyjne obliczanie współrzędnych jest niezbędne w takich dziedzinach jak budownictwo, inżynieria lądowa czy projektowanie sieci infrastrukturalnych. Kluczowe jest także stosowanie odpowiednich narzędzi i oprogramowania geodezyjnego, które umożliwia wykonywanie takich obliczeń z zachowaniem zasad dokładności i rzetelności danych pomiarowych. W geodezji ważne jest, aby dokładnie rozumieć, jak zmiany w przyrostach wpływają na wartości współrzędnych, co może mieć istotne znaczenie dla dalszych prac projektowych.
Błędne odpowiedzi wynikają najczęściej z nieprawidłowego zrozumienia zasad obliczeń w geodezji. Wiele osób może pomylić się, zakładając, że wartości współrzędnych Y są bezpośrednio przekazywane bez uwzględnienia przyrostów, co prowadzi do wniosków opartych na niepełnych danych. Dla przykładu, błędne odpowiedzi mogą sugerować, że wartość Y punktu 2 jest zbliżona do wartości punktu 1, co jest mylne. W rzeczywistości, aby uzyskać prawidłową wartość współrzędnej Y, należy zawsze dodać odpowiedni przyrost Δy. Nieprawidłowe podejście do dodawania wartości lub zaokrąglania może prowadzić do znaczących błędów w obliczeniach, co w praktyce geodezyjnej może skutkować niepoprawnym lokalizowaniem punktów, a w konsekwencji problemami w realizacji projektów budowlanych czy infrastrukturalnych. Kluczowe jest, aby przy każdym obliczeniu opierać się na dokładnych danych i stosować się do procedur, które zapewniają właściwą interpretację wyników. Przykładowo, podstawowe pomyłki mogą wynikać z błędnego zaokrąglania na wcześniejszych etapach obliczeń, co kumuluje błąd do końcowego wyniku. W praktyce, w geodezji bardzo istotne jest utrzymanie wysokiej precyzji pomiarów i zrozumienie, jak różne wartości wpływają na końcowe wyniki pomiarów.